| 释义 |
Delta FunctionDefined as the limit of a class of Delta Sequences. Sometimes called the Impulse Symbol.The most commonly used (equivalent) definitions are
 | (1) |
where  is the Fourier Transform. Some identities include is the Fourier Transform. Some identities include
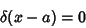 | (5) |
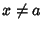 , ,
 | (6) |
 is any Positive number, and is any Positive number, and
 | (7) |
 | (8) |
 | (9) |
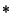 denotes Convolution, denotes Convolution,
 | (10) |
 | (11) |
 | (12) |
 | (13) |
Additional identities are
 | (15) |
 | (16) |
 | (17) |
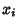 s are the Roots of s are the Roots of 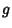 . For example, examine . For example, examine
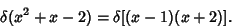 | (18) |
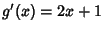 , so , so 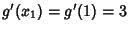 and and  , and we have , and we have
 | (19) |
A Fourier Series expansion of  gives gives
 | (20) |
 | (21) |
The Fourier Transform of the delta function is
 | (23) |
 | (24) |
 | (25) |
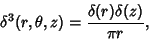 | (26) |
 | (27) |
 | |  | | | (28) |
The delta function also obeys the so-called Sifting Property
 | (29) |
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 481-485, 1985.Spanier, J. and Oldham, K. B. ``The Dirac Delta Function  .'' Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987. .'' Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
|
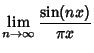

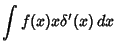
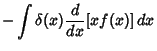

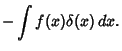

![]() gives
gives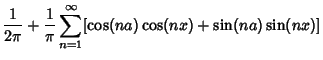

![]() .'' Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
.'' Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.