| 释义 |
Diagonal MatrixA diagonal matrix is a Matrix  of the form of the form
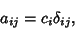 | (1) |
 is the Kronecker Delta, is the Kronecker Delta,  are constants, and there is no summation over indices. The generaldiagonal matrix is therefore Square and of the form are constants, and there is no summation over indices. The generaldiagonal matrix is therefore Square and of the form
 | (2) |
 | (3) |
 | (4) |
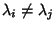 for for 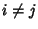 , this can be true only if off-diagonal components vanish.Therefore, A must be diagonal. , this can be true only if off-diagonal components vanish.Therefore, A must be diagonal.
Given a diagonal matrix  , ,
 | (5) |
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 181-184 and 217-229, 1985. |
![]() of the form
of the form


![]() ,
,