“Ultraspherical Polynomial”的概念、定义、习题解题方法及翻译-数学辞典

单词 Ultraspherical Polynomial

释义

Ultraspherical Polynomial

The ultraspherical polynomials are solutions to the Ultraspherical Differential Equation forInteger and . They are generalizations of Legendre Polynomials to-D space and are proportional to (or, depending on the normalization, equal to) the GegenbauerPolynomials , denoted in Mathematica (Wolfram Research, Champaign,IL) GegenbauerC[n,lambda,x]. The ultraspherical polynomials are also Jacobi Polynomials with. They are given by the Generating Function

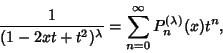(1)

and can be given explicitly by


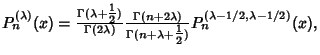	(2)

where

is a Jacobi Polynomial (Szegö 1975, p. 80). The first few ultrasphericalpolynomials are

			(3)
			(4)
			(5)
			(6)

In terms of the Hypergeometric Functions,

			(7)
			(8)
			(9)

They are normalized by

(10)

Derivative identities include

	(11)

	(12)
	(13)
	(14)
	(15)
	(16)
	(17)
	(18)

(Szegö 1975, pp. 80-83).

A Recurrence Relation is

(19)

for

, 3, ....

Special double- Formulas also exist


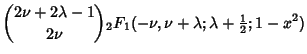			(20)

			(21)

			(22)

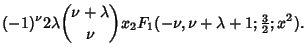			(23)

Special values are given in the following table.

	Special Polynomial
	Legendre Polynomial
1	Chebyshev Polynomial of the Second Kind

Koschmieder (1920) gives representations in terms of Elliptic Functions for and .

See also Birthday Problem, Chebyshev Polynomial of the Second Kind, Elliptic Function, HypergeometricFunction, Jacobi Polynomial

References

Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 643, 1985.

Iyanaga, S. and Kawada, Y. (Eds.). ``Gegenbauer Polynomials (Gegenbauer Functions).'' Appendix A, Table 20.I in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1477-1478, 1980.

Koschmieder, L. ``Über besondere Jacobische Polynome.'' Math. Zeitschrift 8, 123-137, 1920.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 547-549 and 600-604, 1953.

Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。