Uniform Polyhedron
The uniform polyhedra are Polyhedra with identical Vertices. Coxeteret al. (1954) conjectured that there are 75 such polyhedra in which only two faces are allowed to meet at an Edge, and this was subsequently proven. (However, when any Even number of faces may meet, there are 76 polyhedra.)If the five pentagonal Prisms are included, the number rises to 80.
The Vertices of a uniform polyhedron all lie on a Sphere whose center is theirCentroid. The Vertices joined to anotherVertex lie on a Circle.
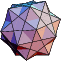
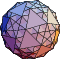
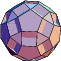
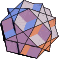
Source code and binary programs for generating and viewing the uniformpolyhedra are also available at http://www.math.technion.ac.il/~rl/kaleido/. The following depictions of the polyhedra were produced by R. Maeder'sUniformPolyhedra.m package for Mathematica![]() (Wolfram Research, Champaign, IL). Due to a limitationin Mathematica's renderer, uniform polyhedra 69, 72, 74, and 75 cannot be displayed using this package.
(Wolfram Research, Champaign, IL). Due to a limitationin Mathematica's renderer, uniform polyhedra 69, 72, 74, and 75 cannot be displayed using this package.
| Name | Dual Polyhedron | Wythoff Symbol | |
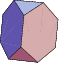
| 1 | Tetrahedron | Tetrahedron | |
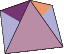
| 2 | Truncated Tetrahedron | Triakis Tetrahedron | |
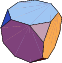
| 3 | Octahemioctahedron | Octahemioctacron | |
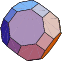
| 4 | Tetrahemihexahedron | Tetrahemihexacron | |
| 5 | Octahedron | Cube | |
| 6 | Cube | Octahedron | |
| 7 | Cuboctahedron | Rhombic Dodecahedron | |
| 8 | Truncated Octahedron | Tetrakis Hexahedron | |
| 9 | Truncated Cube | Triakis Octahedron | |
| 10 | Small Rhombicuboctahedron | Deltoidal Icositetrahedron | |
| 11 | Truncated Cuboctahedron | Disdyakis Dodecahedron | |
| 12 | Snub Cube | Pentagonal Icositetrahedron | |
| 13 | Small Cubicuboctahedron | Small Hexacronic Icositetrahedron | |
| 14 | Great Cubicuboctahedron | Great Hexacronic Icositetrahedron | |
| 15 | Cubohemioctahedron | Hexahemioctahedron | |
| 16 | Cubitruncated Cuboctahedron | Tetradyakis Hexahedron | |
| 17 | Great Rhombicuboctahedron | Great Deltoidal Icositetrahedron | |
| 18 | Small Rhombihexahedron | Small Rhombihexacron | |
| 19 | Stellated Truncated Hexahedron | Great Triakis Octahedron | |
| 20 | Great Truncated Cuboctahedron | Great Disdyakis Dodecahedron | |
| 21 | Great Rhombihexahedron | Great Rhombihexacron | |
| 22 | Icosahedron | Dodecahedron | |
| 23 | Dodecahedron | Icosahedron | |
| 24 | Icosidodecahedron | Rhombic Triacontahedron | |
| 25 | Truncated Icosahedron | Pentakis Dodecahedron | |
| 26 | Truncated Dodecahedron | Triakis Icosahedron | |
| 27 | Small Rhombicosidodecahedron | Deltoidal Hexecontahedron | |
| 28 | Truncated Icosidodecahedron | Disdyakis Triacontahedron | |
| 29 | Snub Dodecahedron | Pentagonal Hexecontahedron | |
| 30 | Small Ditrigonal Icosidodecahedron | Small Triambic Icosahedron | |
| 31 | Small Icosicosidodecahedron | Small Icosacronic Hexecontahedron | |
| 32 | Small Snub Icosicosidodecahedron | Small Hexagonal Hexecontahedron | |
| 33 | Small Dodecicosidodecahedron | Small Dodecacronic Hexecontahedron | |
| 34 | Small Stellated Dodecahedron | Great Dodecahedron | |
| 35 | Great Dodecahedron | Small Stellated Dodecahedron | |
| 36 | Dodecadodecahedron | Medial Rhombic Triacontahedron | |
| 37 | Truncated Great Dodecahedron | Small Stellapentakis Dodecahedron | |
| 38 | Rhombidodecadodecahedron | Medial Deltoidal Hexecontahedron | |
| 39 | Small Rhombidodecahedron | Small Rhombidodecacron | |
| 40 | Snub Dodecadodecahedron | Medial Pentagonal Hexecontahedron | |
| 41 | Ditrigonal Dodecadodecahedron | Medial Triambic Icosahedron | |
| 42 | Great Ditrigonal Dodecicosidodecahedron | Great Ditrigonal Dodecacronic Hexecontahedron | |
| 43 | Small Ditrigonal Dodecicosidodecahedron | Small Ditrigonal Dodecacronic Hexecontahedron | |
| 44 | Icosidodecadodecahedron | Medial Icosacronic Hexecontahedron | |
| 45 | Icositruncated Dodecadodecahedron | Tridyakis Icosahedron | |
| 46 | Snub Icosidodecadodecahedron | Medial Hexagonal Hexecontahedron | |
| 47 | Great Ditrigonal Icosidodecahedron | Great Triambic Icosahedron | |
| 48 | Great Icosicosidodecahedron | Great Icosacronic Hexecontahedron | |
| 49 | Small Icosihemidodecahedron | Small Icosihemidodecacron | |
| 50 | Small Dodecicosahedron | Small Dodecicosacron | |
| 51 | Small Dodecahemidodecahedron | Small Dodecahemidodecacron | |
| 52 | Great Stellated Dodecahedron | Great Icosahedron | |
| 53 | Great Icosahedron | Great Stellated Dodecahedron | |
| 54 | Great Icosidodecahedron | Great Rhombic Triacontahedron | |
| 55 | Great Truncated Icosahedron | Great Stellapentakis Dodecahedron | |
| 56 | Rhombicosahedron | Rhombicosacron | |
| 57 | Great Snub Icosidodecahedron | Great Pentagonal Hexecontahedron | |
| 58 | Small Stellated Truncated Dodecahedron | Great Pentakis Dodecahedron | |
| 59 | Truncated Dodecadodecahedron | Medial Disdyakis Triacontahedron | |
| 60 | Inverted Snub Dodecadodecahedron | Medial Inverted Pentagonal Hexecontahedron | |
| 61 | Great Dodecicosidodecahedron | Great Dodecacronic Hexecontahedron | |
| 62 | Small Dodecahemicosahedron | Small Dodecahemicosacron | |
| 63 | Great Dodecicosahedron | Great Dodecicosacron | |
| 64 | Great Snub Dodecicosidodecahedron | Great Hexagonal Hexecontahedron | |
| 65 | Great Dodecahemicosahedron | Great Dodecahemicosacron | |
| 66 | Great Stellated Truncated Dodecahedron | Great Triakis Icosahedron | |
| 67 | Great Rhombicosidodecahedron | Great Deltoidal Hexecontahedron | |
| 68 | Great Truncated Icosidodecahedron | Great Disdyakis Triacontahedron | |
| 69 | Great Inverted Snub Icosidodecahedron | Great Inverted Pentagonal Hexecontahedron | |
| 70 | Great Dodecahemidodecahedron | Great Dodecahemidodecacron | |
| 71 | Great Icosihemidodecahedron | Great Icosihemidodecacron | |
| 72 | Small Retrosnub Icosicosidodecahedron | Small Hexagrammic Hexecontahedron | |
| 73 | Great Rhombidodecahedron | Great Rhombidodecacron | |
| 74 | Great Retrosnub Icosidodecahedron | Great Pentagrammic Hexecontahedron | |
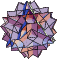
| 75 | Great Dirhombicosidodecahedron | Great Dirhombicosidodecacron | |
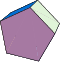
| 76 | Pentagonal Prism | Pentagonal Dipyramid | |
| 77 | Pentagonal Antiprism | Pentagonal Deltahedron | |
| 78 | Pentagrammic Prism | Pentagrammic Dipyramid | |
| 79 | Pentagrammic Antiprism | Pentagrammic Deltahedron | |
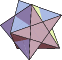
| 80 | Pentagrammic Crossed Antiprism | Pentagrammic Concave Deltahedron |
 |  |  | ||
 |  |  |  | |
 | 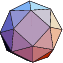 | 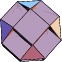 | 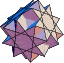 |  |
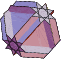 | 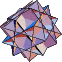 | 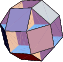 | 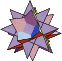 | 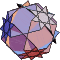 |
 | 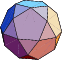 | 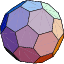 | ||
 | 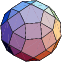 |  | 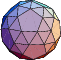 |  |
 |  |  | ||
 | 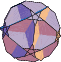 |  | 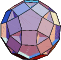 |  |
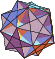 |  |  |  | 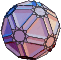 |
 |  |  |  |  |
 | 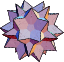 |  | ||
 |  |  |  |  |
 |  |  |  | 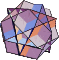 |
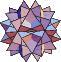 |  |  |  |  |
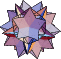 |  |  |  |  |
 |  |  |  |
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 136, 1987. Bulatov, V. ``Compounds of Uniform Polyhedra.''http://www.physics.orst.edu/~bulatov/polyhedra/uniform_compounds/. Bulatov, V. ``Dual Uniform Polyhedra.'' http://www.physics.orst.edu/~bulatov/polyhedra/dual/. Bulatov, V. ``Uniform Polyhedra.'' http://www.physics.orst.edu/~bulatov/polyhedra/uniform/. Coxeter, H. S. M.; Longuet-Higgins, M. S.; and Miller, J. C. P. ``Uniform Polyhedra.'' Phil. Trans. Roy. Soc. London Ser. A 246, 401-450, 1954. Har'El, Z. ``Uniform Solution for Uniform Polyhedra.'' Geometriae Dedicata 47, 57-110, 1993. Har'El, Z. ``Kaleido.'' http://www.math.technion.ac.il/~rl/kaleido/. Har'El, Z. ``Eighty Dual Polyhedra Generated by Kaleido.'' http://www.math.technion.ac.il/~rl/kaleido/dual.html. Har'El, Z. ``Eighty Uniform Polyhedra Generated by Kaleido.'' http://www.math.technion.ac.il/~rl/kaleido/poly.html. Hume, A. ``Exact Descriptions of Regular and Semi-Regular Polyhedra and Their Duals.'' Computing Science Tech. Rept. No. 130. Murray Hill, NJ: AT&T Bell Lab., 1986. Hume, A. Information files on polyhedra. http://netlib.bell-labs.com/netlib/polyhedra/. Johnson, N. W. ``Convex Polyhedra with Regular Faces.'' Canad. J. Math. 18, 169-200, 1966. Maeder, R. E. ``Uniform Polyhedra.'' Mathematica J. 3, 1993. ftp://ftp.inf.ethz.ch/doc/papers/ti/scs/unipoly.ps.gz. Maeder, R. E. Polyhedra.m and PolyhedraExamples Mathematica Maeder, R. E. ``The Uniform Polyhedra.'' http://www.inf.ethz.ch/department/TI/rm/unipoly/. Skilling, J. ``The Complete Set of Uniform Polyhedron.'' Phil. Trans. Roy. Soc. London, Ser. A 278, 111-136, 1975. Virtual Image. ``The Uniform Polyhedra CD-ROM.'' http://ourworld.compuserve.com/homepages/vir_image/html/uniformpolyhedra.html. Wenninger, M. J. Polyhedron Models. New York: Cambridge University Press, pp. 1-10 and 98, 1989. Zalgaller, V. Convex Polyhedra with Regular Faces. New York: Consultants Bureau, 1969. Ziegler, G. M. Lectures on Polytopes. Berlin: Springer-Verlag, 1995.![]() notebooks. http://www.inf.ethz.ch/department/TI/rm/programs.html.
notebooks. http://www.inf.ethz.ch/department/TI/rm/programs.html.
- Pell Polynomial
- Pell Sequence
- Pencil
- Penrose Stairway
- Penrose Tiles
- Penrose Triangle
- Penrose Tribar
- Pentabolo
- Pentacle
- Pentacontagon
- Pentad
- Pentadecagon
- Pentaflake
- Pentagon
- Pentagonal Antiprism
- Pentagonal Cupola
- Pentagonal Deltahedron
- Pentagonal Dipyramid
- Pentagonal Gyrobicupola
- Pentagonal Gyrocupolarotunda
- Pentagonal Hexecontahedron
- Pentagonal Icositetrahedron
- Pentagonal Number
- Pentagonal Orthobicupola
- Pentagonal Orthobirotunda