Osculating Sphere
The center of any Sphere which has a contact of (at least) first-order with a curve 
at a point 
liesin the normal plane to at . The center of any Sphere which has a contact of (at least) second-order with at point , where the Curvature 
, lies on the polar axis of corresponding to . All theseSpheres intersect the Osculating Plane of at along a circle of curvature at . The osculating sphere has center
where
is the unit Normal Vector, 
is the unit Binormal Vector, 
is theRadius of Curvature, and 
is the Torsion, and Radius
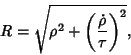
and has contact of (at least) third order with
.See also Curvature, Osculating Plane, Radius of Curvature, Sphere, Torsion (DifferentialGeometry)
References
Kreyszig, E. Differential Geometry. New York: Dover, pp. 54-55, 1991.
- Minkowski Space
- Minkowski Sum
- Minkowski Sum Inequality
- Minor
- Minor Axis
- Minor Graph
- Minus
- Minus or Plus
- Minus Sign
- Minute
- Miquel Circles
- Miquel Equation
- Miquel Point
- Miquel's Theorem
- Miquel Triangle
- Mira Fractal
- Mirimanoff's Congruence
- Mirror Image
- Mirror Plane
- Misère Form
- Mitchell Index
- Miter Surface
- Mittag-Leffler Function
- Mittenpunkt
- Mixed Partial Derivative