| 释义 |
Diophantine Equation--7th PowersThe 2-1 equation
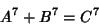 | (1) |
 , and so has no solution. No solutions to the 2-2 equation
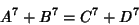 | (2) |
No solutions to the 3-1 or 3-2 equations are known, nor are solutions to the 3-3 equation
 | (3) |
No 4-1, 4-2, or 4-3 solutions are known.Guy (1994, p. 140) asked if a 4-4 equation exists for 7th Powers. An affirmativeanswer was provided by (Ekl 1996),
 | (4) |
 | (5) |
No 5-1, 5-2, or 5-3 solutions are known. Numerical solutions to the 5-4 equation are given by Gloden (1948).The smallest 5-4 solution is
 | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
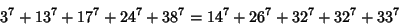 | (11) |
No 6-1, 6-2, or 6-3 solutions are known. A parametric solution to the 6-6 equation was given by Sastry and Rai (1948).The smallest is
 | (12) |
There are no known solutions to the 7-1 equation (Guy 1994, p. 140). A 2-10-10 solution is
(Lander et al. 1967). The smallest 7-3 solution is
 | (14) |
The smallest 8-1 solution is
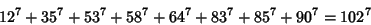 | (15) |
 | (16) |
The smallest 9-1 solution is
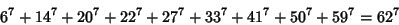 | (17) |
References
Ekl, R. L. ``Equal Sums of Four Seventh Powers.'' Math. Comput. 65, 1755-1756, 1996.Gloden, A. ``Zwei Parameterlösungen einer mehrgeradigen Gleichung.'' Arch. Math. 1, 480-482, 1949. Guy, R. K. ``Sums of Like Powers. Euler's Conjecture.'' §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994. Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. ``A Survey of Equal Sums of Like Powers.'' Math. Comput. 21, 446-459, 1967. Sastry, S. and Rai, T. ``On Equal Sums of Like Powers.'' Math. Student 16, 18-19, 1948.
|
