| 释义 |
Dirac MatricesDefine the 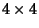 matrices matrices
where 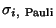 are the Pauli Matrices, I is the Identity Matrix, are the Pauli Matrices, I is the Identity Matrix,  , 2, 3, and , 2, 3, and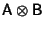 is the matrix Direct Product. Explicitly, is the matrix Direct Product. Explicitly,
These matrices satisfy the anticommutation identities
 | (10) |
 | (11) |
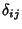 is the Kronecker Delta, the commutation identity is the Kronecker Delta, the commutation identity
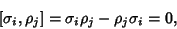 | (12) |
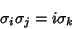 | (13) |
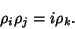 | (14) |
A total of 16 Dirac matrices can be defined via
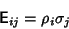 | (15) |
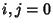 , 1, 2, 3 and where , 1, 2, 3 and where 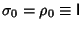 . These matrices satisfy . These matrices satisfy- 1.
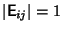 , where , where 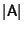 is the Determinant, is the Determinant, - 2.
 , , - 3.
 , making them Hermitian, and therefore unitary, , making them Hermitian, and therefore unitary, - 4.
 , except , except 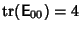 , , - 5. Any two
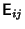 multiplied together yield a Dirac matrix to within a multiplicative factor of multiplied together yield a Dirac matrix to within a multiplicative factor of 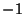 or or 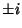 , , - 6. The
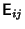 are linearly independent, are linearly independent, - 7. The
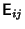 form a complete set, i.e., any form a complete set, i.e., any 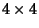 constant matrix may be written as constant matrix may be written as
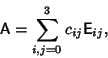 | (16) |
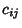 are real or complex and are given by are real or complex and are given by
 | (17) |
(Arfken 1985).
Dirac's original matrices were written 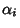 and were defined by and were defined by
for  , 2, 3, giving , 2, 3, giving
The additional matrix
 | (24) |
and
 | (28) |
 , 2, 3 (Arfken 1985) and , 2, 3 (Arfken 1985) and
for  , 2, 3 (Goldstein 1980). , 2, 3 (Goldstein 1980).
Any of the 15 Dirac matrices (excluding the identity matrix) commute with eight Dirac matrices and anticommute with theother eight. Let 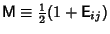 , then , then
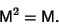 | (31) |
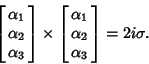 | (32) |
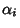 and and 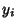 satisfy satisfy
 | (33) |
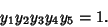 | (34) |
The 16 Dirac matrices form six anticommuting sets of five matrices each: - 1.
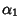 , , 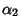 , ,  , ,  , , 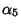 , , - 2.
 , , 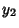 , , 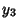 , , 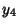 , ,  , , - 3.
 , ,  , ,  , , 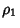 , , 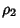 , , - 4.
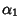 , ,  , ,  , , 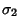 , , 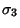 , , - 5.
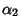 , , 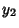 , ,  , , 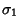 , , 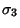 , , - 6.
 , , 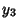 , ,  , , 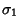 , , 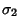 . .
See also Pauli Matrices
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 211-213, 1985.Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, p. 580, 1980.
|
![]() matrices
matrices

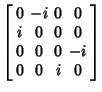
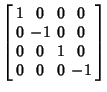

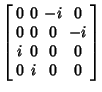
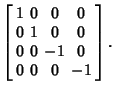
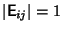 , where
, where 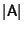 is the Determinant,
is the Determinant, ,
, , making them Hermitian, and therefore unitary,
, making them Hermitian, and therefore unitary, , except
, except 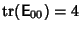 ,
,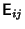 multiplied together yield a Dirac matrix to within a multiplicative factor of
multiplied together yield a Dirac matrix to within a multiplicative factor of 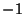 or
or 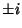 ,
,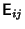 are linearly independent,
are linearly independent,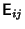 form a complete set, i.e., any
form a complete set, i.e., any  constant matrix may be written aswhere the
constant matrix may be written aswhere the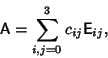
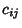 are real or complex and are given by
are real or complex and are given by
![]() and were defined by
and were defined by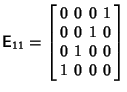

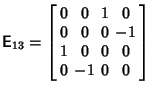
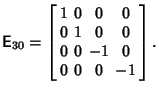

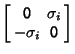

![]() , then
, then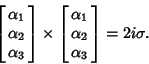
 ,
,  ,
,  ,
,  ,
, 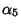 ,
, ,
, 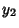 ,
, 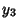 ,
, 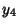 ,
,  ,
, ,
,  ,
,  ,
, 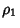 ,
, 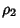 ,
,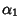 ,
,  ,
,  ,
, 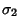 ,
, 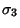 ,
,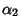 ,
, 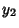 ,
,  ,
, 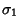 ,
, 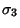 ,
, ,
, 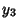 ,
,  ,
, 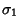 ,
, 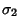 .
.