| 释义 |
Weak Law of Large NumbersAlso known as Bernoulli's Theorem. Let  , ..., , ..., 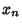 be a sequence of independent and identically distributedrandom variables, each having a Mean be a sequence of independent and identically distributedrandom variables, each having a Mean  and Standard Deviation and Standard Deviation  . Define a new variable . Define a new variable
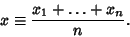 | (1) |
 , the sample mean , the sample mean  equals the population Mean equals the population Mean  of each variable. of each variable.
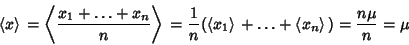 | (2) |
Therefore, by the Chebyshev Inequality, for all  , ,
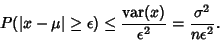 | (4) |
 , it then follows that , it then follows that
 | (5) |
 arbitrarily small; i.e., as arbitrarily small; i.e., as  , the sample Mean is the same as the population Mean. , the sample Mean is the same as the population Mean.
Stated another way, if an event occurs 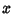 times in times in  Trials and if Trials and if  is the probability of successin a single Trial, then the probability that is the probability of successin a single Trial, then the probability that  for for  an arbitrary Positive quantityapproaches 1 as an arbitrary Positive quantityapproaches 1 as  . . See also Law of Truly Large Numbers, Strong Law of Large Numbers
|
![]() , ...,
, ..., ![]() be a sequence of independent and identically distributedrandom variables, each having a Mean
be a sequence of independent and identically distributedrandom variables, each having a Mean ![]() and Standard Deviation
and Standard Deviation ![]() . Define a new variable
. Define a new variable

![]() times in
times in ![]() Trials and if
Trials and if ![]() is the probability of successin a single Trial, then the probability that
is the probability of successin a single Trial, then the probability that ![]() for
for ![]() an arbitrary Positive quantityapproaches 1 as
an arbitrary Positive quantityapproaches 1 as ![]() .
.