| 释义 |
Eccentric AnomalyThe Angle obtained by drawing the Auxiliary Circle of an Ellipse with center  and Focus and Focus  , anddrawing a Line Perpendicular to the Semimajor Axis and intersecting it at , anddrawing a Line Perpendicular to the Semimajor Axis and intersecting it at  . The Angle . The Angle 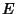 isthen defined as illustrated above. Then for an Ellipse with Eccentricity isthen defined as illustrated above. Then for an Ellipse with Eccentricity 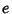 , ,
 | (1) |
 is also given in terms of the distance from the Focus is also given in terms of the distance from the Focus 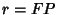 and theSupplement of the Angle from the Semimajor Axis and theSupplement of the Angle from the Semimajor Axis  by by
 | (2) |
 | (3) |
 to obtain to obtain
 | (4) |
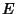 in terms of in terms of  , plug (4) into the equation of the Ellipse , plug (4) into the equation of the Ellipse
 | (5) |
 | (6) |
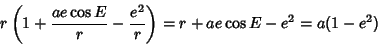 | (7) |
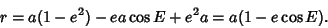 | (8) |
 | (9) |
 where it isrelated to the so-called mean anomaly where it isrelated to the so-called mean anomaly   by Kepler's Equation by Kepler's Equation
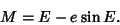 | (10) |
 can also be interpreted as the Area of the shaded region in the above figure (Finch).See also Eccentricity, Ellipse, Kepler's Equation can also be interpreted as the Area of the shaded region in the above figure (Finch).See also Eccentricity, Ellipse, Kepler's Equation
References
Danby, J. M. Fundamentals of Celestial Mechanics, 2nd ed., rev. ed. Richmond, VA: Willmann-Bell, 1988.Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lpc/lpc.html |

![]() and Focus
and Focus ![]() , anddrawing a Line Perpendicular to the Semimajor Axis and intersecting it at
, anddrawing a Line Perpendicular to the Semimajor Axis and intersecting it at ![]() . The Angle
. The Angle ![]() isthen defined as illustrated above. Then for an Ellipse with Eccentricity
isthen defined as illustrated above. Then for an Ellipse with Eccentricity ![]() ,
,