| 释义 |
Ehrhart PolynomialLet  denote an integral convex Polytope of Dimension denote an integral convex Polytope of Dimension  in a lattice in a lattice  , and let , and let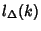 denote the number of Lattice Points in denote the number of Lattice Points in  dilated by a factor of the integer dilated by a factor of the integer  , ,
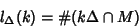 | (1) |
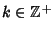 . Then . Then 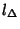 is a polynomial function in is a polynomial function in  of degree of degree  with rational coefficients with rational coefficients
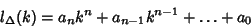 | (2) |
- 1.
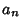 is the Content of is the Content of  . . - 2.
 is half the sum of the Contents of the is half the sum of the Contents of the 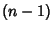 -D faces of -D faces of  . . - 3.
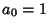 . .
Let 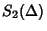 denote the sum of the lattice lengths of the edges of denote the sum of the lattice lengths of the edges of  , then the case , then the case  corresponds toPick's Theorem, corresponds toPick's Theorem,
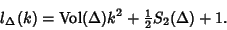 | (3) |
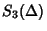 denote the sum of the lattice volumes of the 2-D faces of denote the sum of the lattice volumes of the 2-D faces of  , then the case , then the case 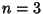 gives gives
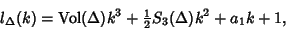 | (4) |
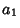 can unfortunately not beinterpreted in terms of the edges of can unfortunately not beinterpreted in terms of the edges of  . The Ehrhart polynomial of the tetrahedron with vertices at(0, 0, 0), ( . The Ehrhart polynomial of the tetrahedron with vertices at(0, 0, 0), ( , 0, 0), (0, , 0, 0), (0, 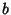 , 0), (0, 0, , 0), (0, 0, 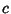 ) iswhere ) iswhere 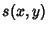 is a Dedekind Sum, is a Dedekind Sum, 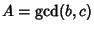 , , 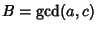 , , 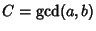 (here, gcd is the Greatest Common Divisor), and (here, gcd is the Greatest Common Divisor), and 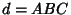 (Pommersheim 1993).See also Dehn Invariant, Pick's Theorem (Pommersheim 1993).See also Dehn Invariant, Pick's Theorem
References
Ehrhart, E. ``Sur une problème de géométrie diophantine linéaire.'' J. Reine angew. Math. 227, 1-29, 1967.MacDonald, I. G. ``The Volume of a Lattice Polyhedron.'' Proc. Camb. Phil. Soc. 59, 719-726, 1963. McMullen, P. ``Valuations and Euler-Type Relations on Certain Classes of Convex Polytopes.'' Proc. London Math. Soc. 35, 113-135, 1977. Pommersheim, J. ``Toric Varieties, Lattices Points, and Dedekind Sums.'' Math. Ann. 295, 1-24, 1993. Reeve, J. E. ``On the Volume of Lattice Polyhedra.'' Proc. London Math. Soc. 7, 378-395, 1957. Reeve, J. E. ``A Further Note on the Volume of Lattice Polyhedra.'' Proc. London Math. Soc. 34, 57-62, 1959. |
![]() denote an integral convex Polytope of Dimension
denote an integral convex Polytope of Dimension ![]() in a lattice
in a lattice ![]() , and let
, and let![]() denote the number of Lattice Points in
denote the number of Lattice Points in ![]() dilated by a factor of the integer
dilated by a factor of the integer ![]() ,
,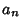 is the Content of
is the Content of  .
. is half the sum of the Contents of the
is half the sum of the Contents of the 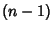 -D faces of
-D faces of  .
.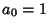 .
.