Zermelo-Fraenkel Axioms
The Zermelo-Fraenkel axioms are the basis for Zermelo-Fraenkel Set Theory. In the following, 
stands forExists, 
for ``is an element of,'' 
for For All, 
for Implies, 
forNot (Negation), 
for And, 
for Or, 
for ``isEquivalent to,'' and 
denotes the union 
of all the sets that are the elements of 
.
- 1. Existence of the empty set:
. - 2. Extensionality axiom:
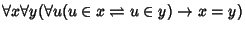. - 3. Unordered pair axiom:
. - 4. Union (or ``sum-set'') axiom:
. - 5. Subset axiom:
. - 6. Replacement axiom: For any set-theoretic formula
,
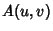- 7. Regularity axiom: For any set-theoretic formula
, 
. - 8. Axiom of Choice:
- 9. Infinity axiom:
.
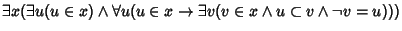- 6'. Axiom of subsets: for any set-theoretic formula ,
,
Abian (1969) proved Consistency and independence of four of the Zermelo-Fraenkel axioms.
See also Zermelo-Fraenkel Set Theory
References
Abian, A. ``On the Independence of Set Theoretical Axioms.'' Amer. Math. Monthly 76, 787-790, 1969. Iyanaga, S. and Kawada, Y. (Eds.). ``Zermelo-Fraenkel Set Theory.'' §35B in Encyclopedic Dictionary of Mathematics, Vol. 1. Cambridge, MA: MIT Press, pp. 134-135, 1980.
- Matroid
- Maurer Rose
- Maximal Ideal
- Maximally Linearly Independent
- Maximal Sum-Free Set
- Maximal Zero-Sum-Free Set
- Maximum
- Maximum Absolute Column Sum Norm
- Maximum Absolute Row Sum Norm
- Maximum Clique Problem
- Maximum Entropy Method
- Maximum Likelihood
- Max Sequence
- Maxwell Distribution
- May's Theorem
- May-Thomason Uniqueness Theorem
- Maze
- Mazur's Theorem
- McCay Circle
- McCoy's Theorem
- McLaughlin Group
- McMohan's Theorem
- McNugget Number
- Mean
- Mean Cluster Count Per Site