| 释义 |
En-FunctionThe 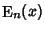 function is defined by the integral function is defined by the integral
 | (1) |
 (Wolfram Research, Champaign, IL) function ExpIntegralE[n,x].Defining (Wolfram Research, Champaign, IL) function ExpIntegralE[n,x].Defining  so that so that 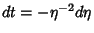 , ,
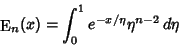 | (2) |
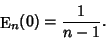 | (3) |
 | (4) |
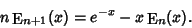 | (5) |
and (5) using integrating by parts, letting
 | (8) |
 | (9) |
Solving (10) for 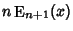 then gives (5). An asymptotic expansion gives then gives (5). An asymptotic expansion gives
 | (11) |
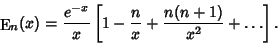 | (12) |
The special case 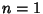 gives gives
 | (13) |
 is the Exponential Integral, which is also equal to is the Exponential Integral, which is also equal to
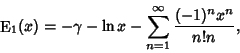 | (14) |
 is the Euler-Mascheroni Constant. is the Euler-Mascheroni Constant.
where  and and 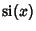 are the Cosine Integral and Sine Integral.See also Cosine Integral, Et-Function, Exponential Integral, Gompertz Constant,Sine Integral are the Cosine Integral and Sine Integral.See also Cosine Integral, Et-Function, Exponential Integral, Gompertz Constant,Sine Integral
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Exponential Integral and Related Functions.'' Ch. 5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 227-233, 1972.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Exponential Integrals.'' §6.3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 215-219, 1992. Spanier, J. and Oldham, K. B. ``The Exponential Integral Ei( ) and Related Functions.'' Ch. 37 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 351-360, 1987. ) and Related Functions.'' Ch. 37 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 351-360, 1987. |
![]() function is defined by the integral
function is defined by the integral

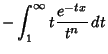



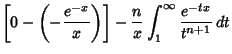


![]() gives
gives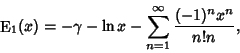
![]() ) and Related Functions.'' Ch. 37 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 351-360, 1987.
) and Related Functions.'' Ch. 37 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 351-360, 1987.