Equivalence Relation
An equivalence relation on a set 
is a Subset of 
, i.e., a collection 
of ordered pairs of elements of, satisfying certain properties. Write ``
'' to mean 
is an element of , and we say ``
is related to
,'' then the properties are
- 1. Reflexive:
for all 
, - 2. Symmetric:
Implies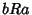 
for all 
- 3. Transitive: and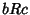
imply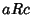 
for all 
,
or 
.See also Equivalence Class, Teichmüller Space
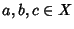References
Stewart, I. and Tall, D. The Foundations of Mathematics. Oxford, England: Oxford University Press, 1977.
- Jonquière's Function
- Jordan Algebra
- Jordan Curve
- Jordan Curve Theorem
- Jordan Decomposition Theorem
- Jordan-Hölder Theorem
- Jordan Measure
- Jordan Polygon
- Jordan's Inequality
- Jordan's Lemma
- Josephus Problem
- Jug
- Jugendtraum
- Juggling
- Julia Fractal
- Julia Set
- Jump
- Jump Angle
- Jumping Champion
- Jung's Theorem
- Just If
- Just One
- Kabon Triangles
- Kac Formula
- Kac Matrix