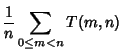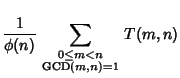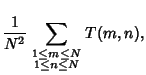| 释义 |
Euclidean AlgorithmAn Algorithm for finding the Greatest Common Divisor of two numbers  and and 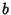 , also called Euclid'salgorithm. It is an example of a P-Problem whose time complexity is bounded by a quadratic function of thelength of the input values (Banach and Shallit). Let , also called Euclid'salgorithm. It is an example of a P-Problem whose time complexity is bounded by a quadratic function of thelength of the input values (Banach and Shallit). Let 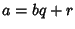 , then find a number , then find a number  which Dividesboth which Dividesboth  and and 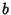 (so that (so that 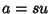 and and 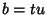 ), then ), then  also Divides also Divides  since since
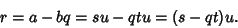 | (1) |
 which Divides which Divides  and and  (so that (so that  and and  ), then ), then  Divides Divides  since since
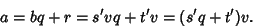 | (2) |
 and and 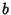 is a common Divisor of is a common Divisor of 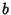 and and  , so the procedure can be iteratedas follows , so the procedure can be iteratedas follows
where  is is 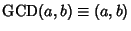 . Lamé showed that the number of steps needed to arrive at the GreatestCommon Divisor for two numbers less than . Lamé showed that the number of steps needed to arrive at the GreatestCommon Divisor for two numbers less than 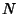 is is
 | (8) |
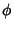 is the Golden Mean, or is the Golden Mean, or 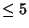 times the number of digits in the smaller number. Numerically, Lamé's expression evaluates to times the number of digits in the smaller number. Numerically, Lamé's expression evaluates to
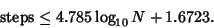 | (9) |
 for all pairs for all pairs  with with 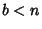 . Kronecker . Kronecker  showed that the shortestapplication of the Algorithm uses least absolute remainders. The Quotients obtained aredistributed as shown in the following table (Wagon 1991). showed that the shortestapplication of the Algorithm uses least absolute remainders. The Quotients obtained aredistributed as shown in the following table (Wagon 1991).| Quotient |  | | 1 | 41.5 | | 2 | 17.0 | | 3 | 9.3 |
For details, see Uspensky and Heaslet (1939) or Knuth (1973). Let 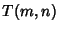 be the number of divisions required tocompute be the number of divisions required tocompute 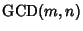 using the Euclidean algorithm, and define using the Euclidean algorithm, and define  if if  . Then . Then
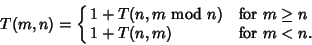 | (10) |
where 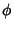 is the Totient Function, is the Totient Function, 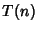 is the average number of divisions when is the average number of divisions when  is fixed and is fixed and  chosen atrandom, chosen atrandom, 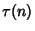 is the average number of divisions when is the average number of divisions when  is fixed and is fixed and  is a random number coprime to is a random number coprime to  , and , and is the average number of divisions when is the average number of divisions when  and and  are both chosen at random in are both chosen at random in  . Norton (1990)showed that . Norton (1990)showed that
 | (14) |
 is the von Mangoldt Function and is the von Mangoldt Function and  is Porter's Constant. Porter (1975) showed that is Porter's Constant. Porter (1975) showed that
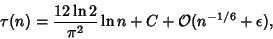 | (15) |
 | (16) |
There exist 22 Quadratic Fields in which there is a Euclidean algorithm (Inkeri 1947). See also Ferguson-Forcade Algorithm
References
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, 1996.Courant, R. and Robbins, H. ``The Euclidean Algorithm.'' §2.4 in Supplement to Ch. 1 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 42-51, 1996. Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 69-70, 1990. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/porter/porter.html Inkeri, K. ``Über den Euklidischen Algorithmus in quadratischen Zahlkörpern.'' Ann. Acad. Sci. Fennicae. Ser. A. I. Math.-Phys. 1947, 1-35, 1947. Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1973. Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1981. Norton, G. H. ``On the Asymptotic Analysis of the Euclidean Algorithm.'' J. Symb. Comput. 10, 53-58, 1990. Porter, J. W. ``On a Theorem of Heilbronn.'' Mathematika 22, 20-28, 1975. Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939. Wagon, S. ``The Ancient and Modern Euclidean Algorithm'' and ``The Extended Euclidean Algorithm.'' §8.1 and 8.2 in Mathematica in Action. New York: W. H. Freeman, pp. 247-252 and 252-256, 1991. |
![]() and
and ![]() , also called Euclid'salgorithm. It is an example of a P-Problem whose time complexity is bounded by a quadratic function of thelength of the input values (Banach and Shallit). Let
, also called Euclid'salgorithm. It is an example of a P-Problem whose time complexity is bounded by a quadratic function of thelength of the input values (Banach and Shallit). Let ![]() , then find a number
, then find a number ![]() which Dividesboth
which Dividesboth ![]() and
and ![]() (so that
(so that ![]() and
and ![]() ), then
), then ![]() also Divides
also Divides ![]() since
since![]() be the number of divisions required tocompute
be the number of divisions required tocompute ![]() using the Euclidean algorithm, and define
using the Euclidean algorithm, and define ![]() if
if ![]() . Then
. Then