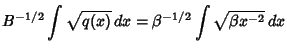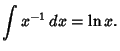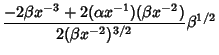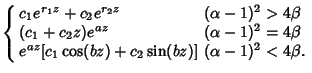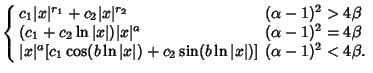| 释义 |
Euler Differential EquationThe general nonhomogeneous equation is
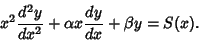 | (1) |
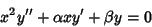 | (2) |
 | (3) |
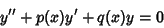 | (4) |
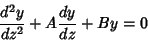 | (5) |
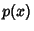 and and 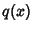 are are
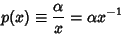 | (6) |
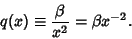 | (7) |
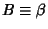 and define and define
Then  is given by is given by
which is a constant. Therefore, the equation becomes a second-order ODE with constant Coefficients
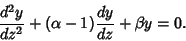 | (10) |
and
The solutions are
In terms of the original variable  , ,
|