| 释义 |
Partial Differential EquationA partial differential equation (PDE) is an equation involving functions and their Partial Derivatives; for example, the Wave Equation
 | (1) |
Fortunately, partial differential equations of second-order are often amenable to analytical solution. Such PDEs are ofthe form
 | (2) |
 | (3) |
If 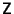 is a Positive Definite Matrix, i.e., det is a Positive Definite Matrix, i.e., det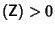 , the PDE is said to be Elliptic. Laplace's Equation and Poisson's Equation are examples. Boundary conditionsare used to give the constraint , the PDE is said to be Elliptic. Laplace's Equation and Poisson's Equation are examples. Boundary conditionsare used to give the constraint 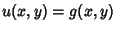 on on 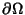 , where , where
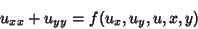 | (4) |
 . .
If det , the PDE is said to be Hyperbolic. The Wave Equation is an example of a hyperbolicpartial differential equation. Initial-boundary conditions are used to give , the PDE is said to be Hyperbolic. The Wave Equation is an example of a hyperbolicpartial differential equation. Initial-boundary conditions are used to give
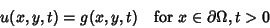 | (5) |
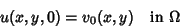 | (6) |
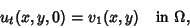 | (7) |
 | (8) |
 . .
If det , the PDE is said to be parabolic. The Heat Conduction Equation equation and otherdiffusion equations , the PDE is said to be parabolic. The Heat Conduction Equation equation and otherdiffusion equations  are examples. Initial-boundary conditions are used to give are examples. Initial-boundary conditions are used to give
 | (9) |
 | (10) |
 | (11) |
 .See also Bäcklund Transformation, Boundary Conditions, Characteristic(Partial Differential Equation), Elliptic Partial Differential Equation, Green's Function, HyperbolicPartial Differential Equation, Integral Transform, Johnson's Equation, Lax Pair,Monge-Ampère Differential Equation, Parabolic Partial DifferentialEquation, Separation of Variables .See also Bäcklund Transformation, Boundary Conditions, Characteristic(Partial Differential Equation), Elliptic Partial Differential Equation, Green's Function, HyperbolicPartial Differential Equation, Integral Transform, Johnson's Equation, Lax Pair,Monge-Ampère Differential Equation, Parabolic Partial DifferentialEquation, Separation of Variables
References
 Partial Differential Equations Partial Differential EquationsArfken, G. ``Partial Differential Equations of Theoretical Physics.'' §8.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 437-440, 1985. Bateman, H. Partial Differential Equations of Mathematical Physics. New York: Dover, 1944. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Partial Differential Equations.'' Ch. 19 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 818-880, 1992. Sobolev, S. L. Partial Differential Equations of Mathematical Physics. New York: Dover, 1989. Sommerfeld, A. Partial Differential Equations in Physics. New York: Academic Press, 1964. Webster, A. G. Partial Differential Equations of Mathematical Physics, 2nd corr. ed. New York: Dover, 1955.
|
![]() is a Positive Definite Matrix, i.e., det
is a Positive Definite Matrix, i.e., det![]() , the PDE is said to be Elliptic. Laplace's Equation and Poisson's Equation are examples. Boundary conditionsare used to give the constraint
, the PDE is said to be Elliptic. Laplace's Equation and Poisson's Equation are examples. Boundary conditionsare used to give the constraint ![]() on
on ![]() , where
, where![]() , the PDE is said to be Hyperbolic. The Wave Equation is an example of a hyperbolicpartial differential equation. Initial-boundary conditions are used to give
, the PDE is said to be Hyperbolic. The Wave Equation is an example of a hyperbolicpartial differential equation. Initial-boundary conditions are used to give![]() , the PDE is said to be parabolic. The Heat Conduction Equation equation and otherdiffusion equations
, the PDE is said to be parabolic. The Heat Conduction Equation equation and otherdiffusion equations ![]() are examples. Initial-boundary conditions are used to give
are examples. Initial-boundary conditions are used to give![]() Partial Differential Equations
Partial Differential Equations