| 释义 |
Fourier SeriesFourier series are expansions of Periodic Functions  in terms of an infinite sum ofSines and Cosines in terms of an infinite sum ofSines and Cosines
 | (1) |
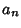 and and  in the sum. The computation andstudy of Fourier series is known as Harmonic Analysis. in the sum. The computation andstudy of Fourier series is known as Harmonic Analysis.
To compute a Fourier series, use the integral identities
 | (2) |
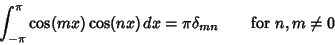 | (3) |
 | (4) |
 | (5) |
 | (6) |
 is the Kronecker Delta. Now, expand your function is the Kronecker Delta. Now, expand your function  as an infinite series of the form as an infinite series of the form
where we have relabeled the  term for future convenience but set term for future convenience but set  and left and left  for for  . Assumethe function is periodic in the interval . Assumethe function is periodic in the interval 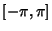 . Now use the orthogonality conditions to obtainandso . Now use the orthogonality conditions to obtainandso
Plugging back into the original series then gives
for  , 2, 3, .... The series expansion converges to the function , 2, 3, .... The series expansion converges to the function  (equal to the original function atpoints of continuity or to the average of the two limits at points of discontinuity) (equal to the original function atpoints of continuity or to the average of the two limits at points of discontinuity)
 | (14) |
Near points of discontinuity, a ``ringing'' known as the Gibbs Phenomenon, illustrated above, occurs.For a function  periodic on an interval periodic on an interval 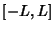 , use a change of variables to transform the interval of integrationto , use a change of variables to transform the interval of integrationto  . Let . Let
Solving for 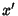 , ,  . Plugging this in gives . Plugging this in gives
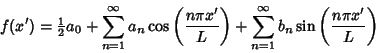 | (17) |
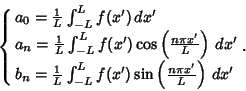 | (18) |
 , then , then  is Odd. (This follows since is Odd. (This follows since  is Odd and an Even Function times an OddFunction is an Odd Function.) Therefore, is Odd and an Even Function times an OddFunction is an Odd Function.) Therefore, 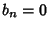 for all for all 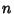 . Similarly, if a function is Odd so that . Similarly, if a function is Odd so that  , then , then 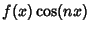 is Odd. (This follows since is Odd. (This follows since  isEven and an Even Function times an Odd Function is an Odd Function.) Therefore, isEven and an Even Function times an Odd Function is an Odd Function.) Therefore,  for all for all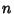 . .
Because the Sines and Cosines form a CompleteOrthogonal Basis, the Superposition Principle holds, and the Fourier series of alinear combination of two functions is the same as the linear combination of the corresponding two series. TheCoefficients for Fourier series expansions for a few common functions are given in Beyer (1987,pp. 411-412) and Byerly (1959, p. 51).
The notion of a Fourier series can also be extended to Complex Coefficients. Consider a real-valued function  . Write . Write
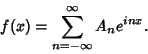 | (19) |
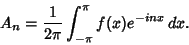 | (21) |
For a function periodic in 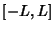 , these become , these become
 | (23) |
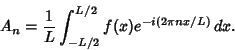 | (24) |
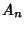 froma discrete variable to a continuous one as the length froma discrete variable to a continuous one as the length  .See also Dirichlet Fourier Series Conditions, Fourier Cosine Series, Fourier Sine Series, FourierTransform, Gibbs Phenomenon, Lebesgue Constants (Fourier Series), Legendre Series, Riesz-FischerTheorem .See also Dirichlet Fourier Series Conditions, Fourier Cosine Series, Fourier Sine Series, FourierTransform, Gibbs Phenomenon, Lebesgue Constants (Fourier Series), Legendre Series, Riesz-FischerTheorem
References
 Fourier Transforms Fourier TransformsArfken, G. ``Fourier Series.'' Ch. 14 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 760-793, 1985. Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987. Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993. Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959. Carslaw, H. S. Introduction to the Theory of Fourier's Series and Integrals, 3rd ed., rev. and enl. New York: Dover, 1950. Davis, H. F. Fourier Series and Orthogonal Functions. New York: Dover, 1963. Dym, H. and McKean, H. P. Fourier Series and Integrals. New York: Academic Press, 1972. Folland, G. B. Fourier Analysis and Its Applications. Pacific Grove, CA: Brooks/Cole, 1992. Groemer, H. Geometric Applications of Fourier Series and Spherical Harmonics. New York: Cambridge University Press, 1996. Körner, T. W. Fourier Analysis. Cambridge, England: Cambridge University Press, 1988. Körner, T. W. Exercises for Fourier Analysis. New York: Cambridge University Press, 1993. Lighthill, M. J. Introduction to Fourier Analysis and Generalised Functions. Cambridge, England: Cambridge University Press, 1958. Morrison, N. Introduction to Fourier Analysis. New York: Wiley, 1994. Sansone, G. ``Expansions in Fourier Series.'' Ch. 2 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 39-168, 1991.
|
![]() in terms of an infinite sum ofSines and Cosines
in terms of an infinite sum ofSines and Cosines

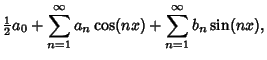
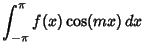
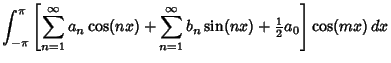


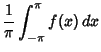




![]() periodic on an interval
periodic on an interval ![]() , use a change of variables to transform the interval of integrationto
, use a change of variables to transform the interval of integrationto ![]() . Let
. Let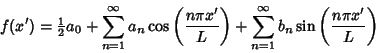
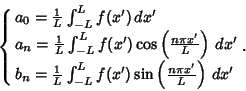
![]() . Write
. Write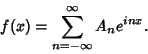
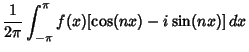
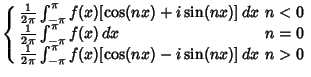
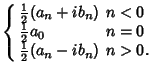

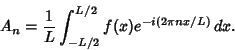
![]() Fourier Transforms
Fourier Transforms