Gauss-Jordan Elimination
A method for finding a Matrix Inverse. To apply Gauss-Jordan elimination, operate on a Matrix
where I is the Identity Matrix, to obtain a Matrix of the form
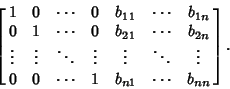
The Matrix
is then the Matrix Inverse of A. The procedure is numerically unstable unless Pivoting (exchanging rowsand columns as appropriate) is used. Picking the largest available element as the pivot is usually a good choice.See also Gaussian Elimination, LU Decomposition, Matrix Equation
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gauss-Jordan Elimination'' and ``Gaussian Elimination with Backsubstitution.'' §2.1 and 2.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 27-32 and 33-34, 1992.
- Napier's Constant
- Napier's Inequality
- Napkin Ring
- Napoleon Points
- Napoleon's Problem
- Napoleon's Theorem
- Napoleon Triangles
- Nappe
- Narcissistic Number
- Nash Equilibrium
- Nash's Theorem
- Nasik Square
- Nasty Knot
- Natural Density
- Natural Equation
- Natural Independence Phenomenon
- Natural Invariant
- Natural Logarithm
- Natural Measure
- Natural Norm
- Natural Number
- Naught
- Navigation Problem
- N-Cluster
- n-Cube