Geometric Construction

In antiquity, geometric constructions of figures and lengths were restricted to use of only a Straightedge andCompass. Although the term ``Ruler'' is sometimes used instead of ``Straightedge,'' no markings whichcould be used to make measurements were allowed according to the Greek prescription. Furthermore, the ``Compass''could not even be used to mark off distances by setting it and then ``walking'' it along, so the Compass had to beconsidered to automatically collapse when not in the process of drawing a Circle.

Because of the prominent place Greek geometric constructions held in Euclid's Elements">Elements,these constructions are sometimes also known as Euclidean Constructions. Suchconstructions lay at the heart of the Geometric Problems of Antiquity of Circle Squaring, CubeDuplication, and Trisection of an Angle. The Greeks were unable to solve these problems, but it was notuntil hundreds of years later that the problems were proved to be actually impossible under the limitations imposed.

Simple algebraic operations such as , , (for a Rational Number), , , and can beperformed using geometric constructions (Courant and Robbins 1996). Other more complicated constructions, such as the solutionof Apollonius' Problem and the construction of Inverse Points can also accomplished.

One of the simplest geometric constructions is the construction of a Bisector of a LineSegment, illustrated above.

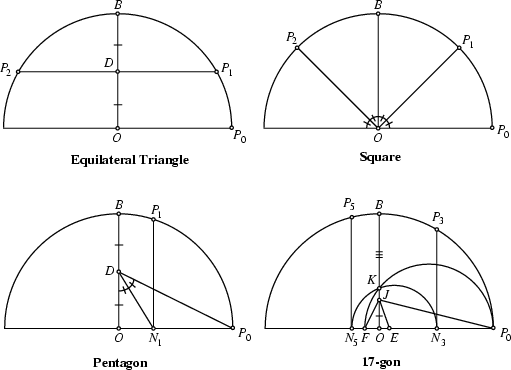
The Greeks were very adept at constructing Gauß tomathematically determine which constructions were possible and which were not. As a result, Gauss determinedthat a series of Polygons (the smallest of which has 17 sides; the Heptadecagon) hadconstructions unknown to the Greeks. Gauss showed that the Constructible Polygons(several of which are illustrated above) were closely related to numbers called the Fermat Primes.

Wernick (1982) gave a list of 139 sets of three located points from which a Triangle was to be constructed. Of Wernick'soriginal list of 139 problems, 20 had not yet been solved as of 1996 (Meyers 1996).

It is possible to construct Rational Numbers and Euclidean Numbers usinga Straightedge and Compass construction. In general, the term for a number which can be constructed using aCompass and Straightedge is a Constructible Number. Some Irrational Numbers,but no Transcendental Numbers, can be constructed.

It turns out that all constructions possible with a Compass and Straightedge can be done with a Compassalone, as long as a line is considered constructed when its two endpoints are located. The reverse is also true, since JacobSteiner showed that all constructions possible with Straightedge and Compass can be done using only astraightedge, as long as a fixed Circle and its center (or two intersecting Circles without theircenters, or three nonintersecting Circles) have been drawn beforehand. Such a construction is known as aSteiner Construction.

Geometrography is a quantitative measure of the simplicity of a geometric construction. It reduces geometricconstructions to five types of operations, and seeks to reduce the total number of operations (called the``Simplicity'') needed to effect a geometric construction.

Dixon (1991, pp. 34-51) gives approximate constructions for some figures (the Heptagon and Nonagon) andlengths (Ramanujan (1913-14) and Olds (1963) give geometricconstructions for . Gardner (1966, pp. 92-93) gives a geometric construction for

References

Geometric Construction

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 96-97, 1987.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 191-202, 1996.

Courant, R. and Robbins, H. ``Geometric Constructions. The Algebra of Number Fields.'' Ch. 3 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 117-164, 1996.

Dantzig, T. Number, The Language of Science. New York: Macmillan, p. 316, 1954.

Dixon, R. Mathographics. New York: Dover, 1991.

Eppstein, D. ``Geometric Models.''http://www.ics.uci.edu/~eppstein/junkyard/model.html.

Gardner, M. ``The Transcendental Number Pi.'' Ch. 8 in Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, 1966.

Gardner, M. ``Mascheroni Constructions.'' Ch. 17 in Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, pp. 216-231, 1979.

Herterich, K. Die Konstruktion von Dreiecken. Stuttgart: Ernst Klett Verlag, 1986.

Krötenheerdt, O. ``Zur Theorie der Dreieckskonstruktionen.'' Wissenschaftliche Zeitschrift der Martin-Luther-Univ. Halle-Wittenberg, Math. Naturw. Reihe 15, 677-700, 1966.

Meyers, L. F. ``Update on William Wernick's `Triangle Constructions with Three Located Points.''' Math. Mag. 69, 46-49, 1996.

Olds, C. D. Continued Fractions. New York: Random House, pp. 59-60, 1963.

Petersen, J. ``Methods and Theories for the Solution of Problems of Geometrical Constructions.'' Reprinted in String Figures and Other Monographs. New York: Chelsea, 1960.

Plouffe, S.. ``The Computation of Certain Numbers Using a Ruler and Compass.'' Dec. 12, 1997.http://www.research.att.com/~njas/sequences/JIS/compass.html.

Posamentier, A. S. and Wernick, W. Advanced Geometric Constructions. Palo Alto, CA: Dale Seymour Pub., 1988.

Ramanujan, S. ``Modular Equations and Approximations to .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.

Wernick, W. ``Triangle Constructions with Three Located Points.'' Math. Mag. 55, 227-230, 1982.

• Realizer
• Real Line
• Real Matrix
• Real Number
• Real Part
• Real Polynomial
• Real Projective Plane
• Real Quadratic Field
• Rearrangement Theorem
• Reciprocal
• Reciprocal Difference
• Reciprocal Polyhedron
• Reciprocating Sphere
• Reciprocation
• Reciprocity Theorem
• Rectangle
• Rectangle Function
• Rectangle Squaring
• Rectangular Coordinates
• Rectangular Distribution
• Rectangular Hyperbola
• Rectangular Parallelepiped
• Rectangular Projection
• Rectifiable Current
• Rectifiable Set