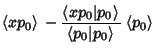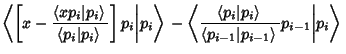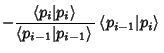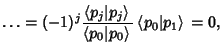| 释义 |
Gram-Schmidt OrthonormalizationA procedure which takes a nonorthogonal set of Linearly Independent functions and constructs an OrthogonalBasis over an arbitrary interval with respect to an arbitrary Weighting Function 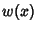 . Given an original setof linearly independent functions . Given an original setof linearly independent functions  , let , let  denote the orthogonalized (but not normalized) functions and denote the orthogonalized (but not normalized) functions and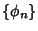 the orthonormalized functions. the orthonormalized functions.
Take
 | (3) |
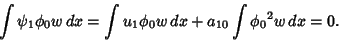 | (4) |
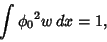 | (5) |
 | (6) |
 | (7) |
 | (8) |
 | (9) |
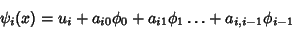 | (10) |
 | (11) |
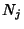 instead of 1, then instead of 1, then
 | (12) |
 | (13) |
 | (14) |
Orthogonal Polynomials are especially easy to generate using Gram-Schmidt Orthonormalization. Use the notation
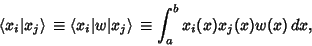 | (15) |
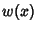 is a Weighting Function, and define the first few Polynomials, is a Weighting Function, and define the first few Polynomials,
As defined,  and and  are Orthogonal Polynomials, as can be seen from are Orthogonal Polynomials, as can be seen from
Now use the Recurrence Relation
 | (19) |
To verify that this procedure does indeed produce Orthogonal Polynomials, examine
since 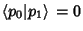 . Therefore, all the Polynomials . Therefore, all the Polynomials  are orthogonal. Many commonOrthogonal Polynomials of mathematical physics can be generated in this manner. However, the process isnumerically unstable (Golub and van Loan 1989).See also Gram Determinant, Gram's Inequality, Orthogonal Polynomials are orthogonal. Many commonOrthogonal Polynomials of mathematical physics can be generated in this manner. However, the process isnumerically unstable (Golub and van Loan 1989).See also Gram Determinant, Gram's Inequality, Orthogonal Polynomials
References
Arfken, G. ``Gram-Schmidt Orthogonalization.'' §9.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 516-520, 1985.Golub, G. H. and van Loan, C. F. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins, 1989. |
![]() . Given an original setof linearly independent functions
. Given an original setof linearly independent functions ![]() , let
, let ![]() denote the orthogonalized (but not normalized) functions and
denote the orthogonalized (but not normalized) functions and![]() the orthonormalized functions.
the orthonormalized functions.