“Ackermann Function”的概念、定义、习题解题方法及翻译-数学辞典

单词

Ackermann Function

释义

Ackermann Function

The Ackermann function is the simplest example of a well-defined Total Function which isComputable but not Primitive Recursive, providing acounterexample to the belief in the early 1900s that every Computable Function was also PrimitiveRecursive (Dötzel 1991). It grows faster than an exponential function, or even a multipleexponential function. The Ackermann function is defined by

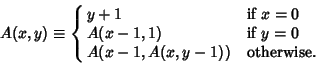(1)

Special values for Integer

include

			(2)
			(3)
			(4)
			(5)
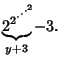			(6)

Expressions of the latter form are sometimes called Power Towers.

follows trivially from thedefinition.

can be derived as follows,




			(7)

has a similar derivation,



			(8)

Buck (1963) defines a related function using the same fundamental Recurrence Relation (with arguments flipped from Buck's convention)

(9)

but with the slightly different boundary values

			(10)
			(11)
			(12)
			(13)

Buck's recurrence gives

			(14)
			(15)
			(16)
			(17)

Taking

gives the sequence 1, 2, 4, 16, 65536,

, .... Defining

for

, 1, ... then gives 1, 3, 4, 8, 65536,

, ... (Sloane's A001695), where

, atruly huge number!

See also Ackermann Number, Computable Function, Goodstein Sequence, Power Tower,Primitive Recursive Function, TAK Function, Total Function

References

Buck, R. C. ``Mathematical Induction and Recursive Definitions.'' Amer. Math. Monthly 70, 128-135, 1963.

Dötzel, G. ``A Function to End All Functions.'' Algorithm: Recreational Programming 2.4, 16-17, 1991.

Kleene, S. C. Introduction to Metamathematics. New York: Elsevier, 1971.

Péter, R. Rekursive Funktionen. Budapest: Akad. Kiado, 1951.

Reingold, E. H. and Shen, X. ``More Nearly Optimal Algorithms for Unbounded Searching, Part I: The Finite Case.'' SIAM J. Comput. 20, 156-183, 1991.

Rose, H. E. Subrecursion, Functions, and Hierarchies. New York: Clarendon Press, 1988.

Sloane, N. J. A. SequenceA001695/M2352in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Smith, H. J. ``Ackermann's Function.'' http://pweb.netcom.com/~hjsmith/Ackerman.html.

Spencer, J. ``Large Numbers and Unprovable Theorems.'' Amer. Math. Monthly 90, 669-675, 1983.

Tarjan, R. E. Data Structures and Network Algorithms. Philadelphia PA: SIAM, 1983.

Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 11, 227, and 232, 1991.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。