| 释义 |
GroupA group  is defined as a finite or infinite set of Operands (called ``elements'') is defined as a finite or infinite set of Operands (called ``elements'') 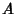 , ,  , , 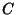 , ... thatmay be combined or ``multiplied'' via a Binary Operator to form well-defined products and which furthermore satisfy the followingconditions: , ... thatmay be combined or ``multiplied'' via a Binary Operator to form well-defined products and which furthermore satisfy the followingconditions: - 1. Closure: If
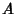 and and  are two elements in are two elements in  , then the product , then the product 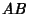 is also in is also in  . . - 2. Associativity: The defined multiplication is associative, i.e., for all
 , ,  . . - 3. Identity: There is an Identity Element
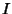 (a.k.a. (a.k.a.  , , 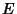 , or , or  ) such that ) such that  for every element for every element  . . - 4. Inverse: There must be an inverse or reciprocal of each element. Therefore, the set must contain anelement
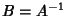 such that such that  for each element of for each element of  . .
A group is therefore a Monoid for which every element is invertible. A group must contain at least one element.
The study of groups is known as Group Theory. If there are a finite number of elements, the group is called aFinite Group and the number of elements is called the Order of the group.
Since each element 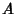 , ,  , , 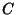 , ..., , ...,  , and , and  is a member of the group, group property 1 requires thatthe product is a member of the group, group property 1 requires thatthe product
 | (1) |
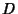 to to 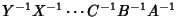 , ,
 | (2) |
 | (4) |
 | (5) |
 | (6) |
An Irreducible Representation of a group is a representation for which there exists no Unitary Transformationwhich will transform the representation Matrix into block diagonal form. The Irreducible Representation has someremarkable properties. Let the Order of a Group be 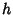 , and the dimension of the , and the dimension of the  threpresentation (the order of each constituent matrix) be threpresentation (the order of each constituent matrix) be  (a Positive Integer). Let any operation be denoted (a Positive Integer). Let any operation be denoted , and let the , and let the  th row and th row and  th column of the matrix corresponding to a matrix th column of the matrix corresponding to a matrix  in the in the  th IrreducibleRepresentation be th IrreducibleRepresentation be  . The following properties can be derived from the Group Orthogonality Theorem, . The following properties can be derived from the Group Orthogonality Theorem,
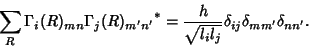 | (7) |
- 1. The Dimensionality Theorem:
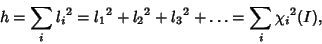 | (8) |
 must be a Positive Integer and must be a Positive Integer and 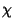 is the Character (trace) of therepresentation. is the Character (trace) of therepresentation. - 2. The sum of the squares of the Characters in any Irreducible Representation
 equals equals 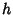 , ,
 | (9) |
- 3. Orthogonality of different representations
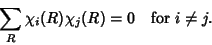 | (10) |
- 4. In a given representation, reducible or irreducible, the Characters of allMatrices belonging to operations in the same class are identical (but differ from those in otherrepresentations).
- 5. The number of Irreducible Representations of a Group is equal to thenumber of Conjugacy Classes in the Group. This number is the dimension of the
 Matrix (although some may have zero elements). Matrix (although some may have zero elements). - 6. A one-dimensional representation with all 1s (totally symmetric) will always exist for any Group.
- 7. A 1-D representation for a Group with elements expressed as Matrices can be found by takingthe Characters of the Matrices.
- 8. The number
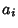 of Irreducible Representations of Irreducible Representations  present in a reduciblerepresentation present in a reduciblerepresentation  is given by is given by
 | (11) |
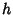 is the Order of the Group and the sum must be taken over all elements in each class. Written explicitly, is the Order of the Group and the sum must be taken over all elements in each class. Written explicitly,
 | (12) |
 is the Character of a single entry in the Character Table and is the Character of a single entry in the Character Table and  isthe number of elements in the corresponding Conjugacy Class. isthe number of elements in the corresponding Conjugacy Class.
See also Abelian Group, Adéle Group, Affine Group, Alternating Group, ArtinianGroup, Aschbacher's Component Theorem, Bp-Theorem, Baby Monster Group, BettiGroup, Bimonster, Bordism Group, Braid Group, Brauer Group, Burnside Problem, Center(Group), Centralizer, Character (Group), Character (Multiplicative), Chevalley Groups,Classical Groups, Cobordism Group, Cohomotopy Group, Component, Conjugacy Class,Coset, Conway Groups, Coxeter Group, Cyclic Group, Dihedral Group, DimensionalityTheorem, Dynkin Diagram, Elliptic Group Modulo p, Engel's Theorem, Euclidean Group,Feit-Thompson Theorem, Finite Group, Fischer Groups, Fischer's Baby Monster Group,Fundamental Group, General Linear Group, General Orthogonal Group, General Unitary Group,Global C(G;T) Theorem, Groupoid, Group Orthogonality Theorem,Hall-Janko Group, Hamiltonian Group, Harada-Norton Group, Heisenberg Group, Held Group,Hermann-Mauguin Symbol, Higman-Sims Group, Homeomorphic Group, Hypergroup, IcosahedralGroup, Irreducible Representation, Isomorphic Groups, Janko Groups, Jordan-HölderTheorem, Kleinian Group, Kummer Group, Lp'-BalanceTheorem, Lagrange's Group Theorem, Local Group Theory, Linear Group, Lyons Group, MathieuGroups, Matrix Group, McLaughlin Group, Möbius Group, Modular Group,Modulo Multiplication Group, Monodromy Group, Monoid, Monster Group, Mulliken Symbols,Néron-Severi Group, NilpotentGroup, Noncommutative Group, Normal Subgroup, Normalizer, O'Nan Group, Octahedral Group,Order (Group), Orthogonal Group, Orthogonal Rotation Group, Outer Automorphism Group,p-Group, p'-Group, p-Layer, Point Groups, Positive Definite Function, PrimeGroup, Projective General Linear Group, Projective General Orthogonal Group, Projective General UnitaryGroup, Projective Special Linear Group, Projective Special Orthogonal Group, Projective Special UnitaryGroup, Projective Symplectic Group, Pseudogroup, Quasigroup, QuasisimpleGroup, Quasithin Theorem, Quasi-Unipotent Group, Representation, Residue Class, Rubik's Cube, Rudvalis Group,Schönflies Symbol, Schur Multiplier, Semisimple, Signalizer FunctorTheorem, Selmer Group, Semigroup, Simple Group, Solvable Group, Space Groups, SpecialLinear Group, Special Orthogonal Group, Special Unitary Group, Sporadic Group, Stochastic Group,Strongly Embedded Theorem, Subgroup, Subnormal, Support, Suzuki Group, SymmetricGroup, Symplectic Group, Tetrahedral Group, Thompson Group, Tightly Embedded, Tits Group,Triangular Symmetry Group, Twisted Chevalley Groups, Unimodular Group, Unipotent, UnitaryGroup, Viergruppe, von Dyck's Theorem
References Group Theory Group TheoryArfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 237-276, 1985. Farmer, D. Groups and Symmetry. Providence, RI: Amer. Math. Soc., 1995.  Weisstein, E. W. ``Groups.'' Mathematica notebook Groups.m. Weisstein, E. W. ``Groups.'' Mathematica notebook Groups.m.
Weyl, H. The Classical Groups: Their Invariants and Representations. Princeton, NJ: Princeton University Press, 1997. Wybourne, B. G. Classical Groups for Physicists. New York: Wiley, 1974.
|
![]() is defined as a finite or infinite set of Operands (called ``elements'')
is defined as a finite or infinite set of Operands (called ``elements'') ![]() ,
, ![]() ,
, ![]() , ... thatmay be combined or ``multiplied'' via a Binary Operator to form well-defined products and which furthermore satisfy the followingconditions:
, ... thatmay be combined or ``multiplied'' via a Binary Operator to form well-defined products and which furthermore satisfy the followingconditions: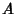 and
and  are two elements in
are two elements in  , then the product
, then the product 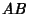 is also in
is also in  .
. ,
,  .
.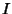 (a.k.a.
(a.k.a.  ,
, 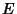 , or
, or  ) such that
) such that  for every element
for every element  .
.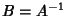 such that
such that  for each element of
for each element of  .
.![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() , and
, and ![]() is a member of the group, group property 1 requires thatthe product
is a member of the group, group property 1 requires thatthe product![]() , and the dimension of the
, and the dimension of the ![]() threpresentation (the order of each constituent matrix) be
threpresentation (the order of each constituent matrix) be ![]() (a Positive Integer). Let any operation be denoted
(a Positive Integer). Let any operation be denoted![]() , and let the
, and let the ![]() th row and
th row and ![]() th column of the matrix corresponding to a matrix
th column of the matrix corresponding to a matrix ![]() in the
in the ![]() th IrreducibleRepresentation be
th IrreducibleRepresentation be ![]() . The following properties can be derived from the Group Orthogonality Theorem,
. The following properties can be derived from the Group Orthogonality Theorem,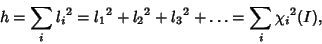
 must be a Positive Integer and
must be a Positive Integer and 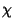 is the Character (trace) of therepresentation.
is the Character (trace) of therepresentation. equals
equals 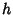 ,
,
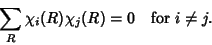
 Matrix (although some may have zero elements).
Matrix (although some may have zero elements).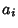 of Irreducible Representations
of Irreducible Representations  present in a reduciblerepresentation
present in a reduciblerepresentation  is given bywhere
is given bywhere
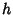 is the Order of the Group and the sum must be taken over all elements in each class. Written explicitly,where
is the Order of the Group and the sum must be taken over all elements in each class. Written explicitly,where
 is the Character of a single entry in the Character Table and
is the Character of a single entry in the Character Table and  isthe number of elements in the corresponding Conjugacy Class.
isthe number of elements in the corresponding Conjugacy Class.![]() Group Theory
Group Theory![]() Weisstein, E. W. ``Groups.'' Mathematica notebook Groups.m.
Weisstein, E. W. ``Groups.'' Mathematica notebook Groups.m.