| 释义 |
Harmonic FunctionAny real-valued function  with continuous second Partial Derivatives which satisfiesLaplace's Equation with continuous second Partial Derivatives which satisfiesLaplace's Equation
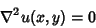 | (1) |
 where they reduce the study of a 3-component Vector Field toa 1-component Scalar Function. A scalar harmonic function is called a Scalar Potential, and a vectorharmonic function is called a Vector Potential. where they reduce the study of a 3-component Vector Field toa 1-component Scalar Function. A scalar harmonic function is called a Scalar Potential, and a vectorharmonic function is called a Vector Potential.
To find a class of such functions in the Plane, write the Laplace's Equation in Polar Coordinates
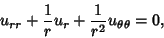 | (2) |
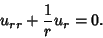 | (3) |
 , ,
 | (4) |
 | (5) |
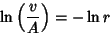 | (6) |
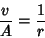 | (7) |
 | (8) |
 | (9) |
 | (10) |
 | (11) |
Other solutions may be obtained by differentiation, such as
and
 | (16) |
The Poisson Kernel
 | (19) |
References
 Potential Theory Potential TheoryAsh, J. M. (Ed.) Studies in Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1976. Axler, S.; Pourdon, P.; and Ramey, W. Harmonic Function Theory. Springer-Verlag, 1992. Benedetto, J. J. Harmonic Analysis and Applications. Boca Raton, FL: CRC Press, 1996. Cohn, H. Conformal Mapping on Riemann Surfaces. New York: Dover, 1980.
|
![]() with continuous second Partial Derivatives which satisfiesLaplace's Equation
with continuous second Partial Derivatives which satisfiesLaplace's Equation 
![]() Potential Theory
Potential Theory