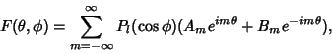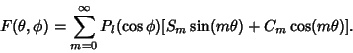| 释义 |
Helmholtz Differential Equation--Spherical SurfaceOn the surface of a Sphere, attempt Separation of Variables in Spherical Coordinates by writing
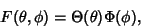 | (1) |
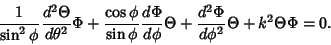 | (2) |
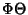 , ,
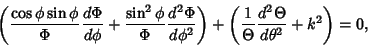 | (3) |
 | (4) |
 must be an Integer. The solution may then be defined either asa Complex function must be an Integer. The solution may then be defined either asa Complex function
 | (5) |
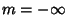 , ..., , ...,  , or as a sum of Real sine and cosine functions , or as a sum of Real sine and cosine functions
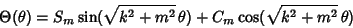 | (6) |
 , ..., , ...,  . Plugging (4) into (3) gives . Plugging (4) into (3) gives
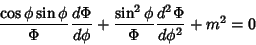 | (7) |
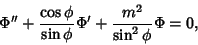 | (8) |
 with with
 | (9) |
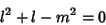 | (10) |
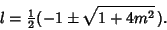 | (11) |
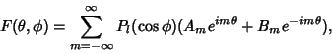 | (12) |
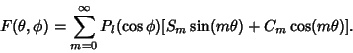 | (13) |
 . However, on the surface of a sphere, it is usual to expresssolutions in terms of the Spherical Harmonics derived for the 3-D spherical case, which depend onthe two variables . However, on the surface of a sphere, it is usual to expresssolutions in terms of the Spherical Harmonics derived for the 3-D spherical case, which depend onthe two variables 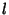 and and  . . |