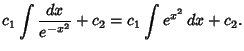| 释义 |
Hermite Differential Equation
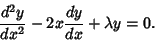 | (1) |
 . It can be solved using the series method . It can be solved using the series method
 | (2) |
 | (3) |
 | (4) |
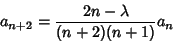 | (5) |
 , 2, .... Since (4) is just a special case of (5), , 2, .... Since (4) is just a special case of (5),
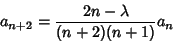 | (6) |
 , 1, .... The linearly independent solutions are then , 1, .... The linearly independent solutions are then
If  , 4, 8, ..., then , 4, 8, ..., then  terminates with the Power terminates with the Power  , and , and  (normalized so thatthe Coefficient of (normalized so thatthe Coefficient of  is is 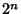 ) is the regular solution to the equation, known as the Hermite Polynomial. If ) is the regular solution to the equation, known as the Hermite Polynomial. If , 6, 10, ..., then , 6, 10, ..., then  terminates with the Power terminates with the Power  , and , and  (normalized sothat the Coefficient of (normalized sothat the Coefficient of  is is 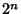 ) is the regular solution to the equation, known as the Hermite Polynomial. ) is the regular solution to the equation, known as the Hermite Polynomial.
If 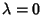 , then Hermite's differential equation becomes , then Hermite's differential equation becomes
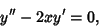 | (9) |
 and so has solution and so has solution
|




![]() , then Hermite's differential equation becomes
, then Hermite's differential equation becomes