“Hölder Sum Inequality”的概念、定义、习题解题方法及翻译-数学辞典

单词

Hölder Sum Inequality

释义

Hölder Sum Inequality

with

, then

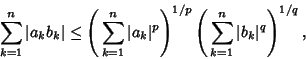
with equality when

. If

, this becomes the Cauchy Inequality.

References

Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 11, 1972.

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, p. 1092, 1979.

Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities, 2nd ed. Cambridge, England: Cambridge University Press, pp. 10-15, 1988.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。