Interspersion
An Array 
, 
of Positive Integers is called an interspersion if
- 1. The rows of
comprise a Partition of the Positive Integers, - 2. Every row of is an increasing sequence,
- 3. Every column of is a (possibly Finite) increasing sequence,
- 4. If
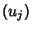and 
are distinct rows of and if 
and 
are any indices for which
, then 
.
is an interspersion, then it is a Dispersion. If an array
is an interspersion, then the sequence 
given by 
for some 
is a FractalSequence. Examples of interspersion are the Stolarsky Array and Wythoff Array.See also Dispersion (Sequence), Fractal Sequence, Stolarsky Array
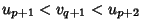References
Kimberling, C. ``Interspersions and Dispersions.'' Proc. Amer. Math. Soc. 117, 313-321, 1993. Kimberling, C. ``Fractal Sequences and Interspersions.'' Ars Combin. 45, 157-168, 1997.
- Hypervolume
- Hypocycloid
- Hypocycloid--3-Cusped
- Hypocycloid--4-Cusped
- Hypocycloid Evolute
- Hypocycloid Involute
- Hypocycloid Pedal Curve
- Hypoellipse
- Hypotenuse
- Hypothesis
- Hypothesis Testing
- Hypotrochoid
- Hypotrochoid Evolute
- Hyzer's Illusion
- Hénon Attractor
- Hénon-Heiles Equation
- Hénon Map
- Hölder Condition
- Hölder Integral Inequality
- Hölder Sum Inequality
- i
- I
- Iamond
- Ice Fractal
- Icosagon