“Inversion”的概念、定义、习题解题方法及翻译-数学辞典

单词

Inversion

释义

Inversion

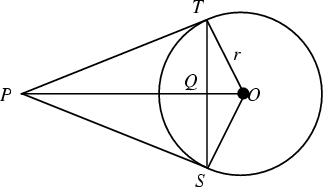
Inversion is the process of transforming points to their Inverse Points. This sort of inversion was firstsystematically investigated by Jakob Steiner. Two points are said to be inverses with respect to an InversionCircle with Inversion Center and Inversion Radius if and are line segmentssymmetric about and tangent to the Circle, and is the intersection of and . The curveto which a given curve is transformed under inversion is called its Inverse Curve.

Note that a point on the Circumference of the Inversion Circle is its own inverse point. The inverse points obey

(1)

(2)

where

is called the Power. The equation for the inverse of the point

relative to theInversion Circle with Inversion Center

and inversion radius

is therefore

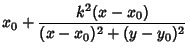			(3)
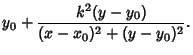			(4)

In vector form,

(5)

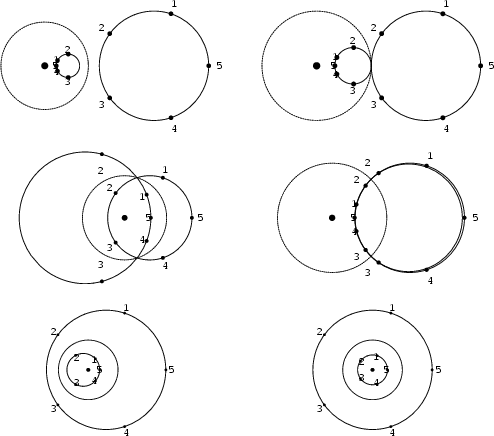
Any Angle inverts to an opposite Angle.

Treating Lines as Circles of Infinite Radius, allCircles invert to Circles. Furthermore, any two nonintersecting circles can beinverted into concentric circles by taking the Inversion Center at one of the two limiting points (Coxeter 1969),and Orthogonal Circles invert to Orthogonal Circles (Coxeter 1969).

The inverse of a Circle of Radius with Center with respect to an inversion circle withInversion Center and Inversion Radius is another Circle with Center and Radius , where

(6)

The above plot shows a checkerboard centered at (0, 0) and its inverse about a small circle also centered at (0, 0)(Dixon 1991).

See also Arbelos, Hexlet, Inverse Curve, Inversion Circle, Inversion Operation, InversionRadius, Inversive Distance, Inversive Geometry, Midcircle, Pappus Chain, PeaucellierInversor, Polar, Pole (Geometry), Power (Circle), Radical Line, Steiner Chain,Steiner's Porism

References

Courant, R. and Robbins, H. ``Geometrical Transformations. Inversion.'' §3.4 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 140-146, 1996.

Coxeter, H. S. M. ``Inversion in a Circle'' and ``Inversion of Lines and Circles.'' §6.1 and 6.3 in Introduction to Geometry, 2nd ed. New York: Wiley, p. 77-83, 1969.

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 108-114, 1967.

Dixon, R. ``Inverse Points and Mid-Circles.'' §1.6 in Mathographics. New York: Dover, pp. 62-73, 1991.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 43-57, 1929.

Lockwood, E. H. ``Inversion.'' Ch. 23 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 176-181, 1967.

Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 25-31, 1990.

Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。