| 释义 |
Jacobi SymbolThe product of Legendre Symbols 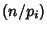 for each of the Prime factors for each of the Prime factors  such that such that , denoted , denoted 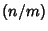 . When . When 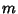 is a Prime, the Jacobi symbol reduces to the Legendre Symbol. TheJacobi symbol satisfies the same rules as the Legendre Symbol is a Prime, the Jacobi symbol reduces to the Legendre Symbol. TheJacobi symbol satisfies the same rules as the Legendre Symbol
 | (1) |
 | (2) |
 | (3) |
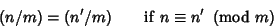 | (4) |
 | (5) |
 | (6) |
 | (7) |
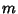 and and  Relatively Prime Odd Integers with Relatively Prime Odd Integers with  , ,
 | (8) |
 or or 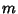 is Even. is Even.
Bach and Shallit (1996) show how to compute the Jacobi symbol in terms of the Simple Continued Fraction of aRational Number  . . See also Kronecker Symbol
References
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, pp. 343-344, 1996.Guy, R. K. ``Quadratic Residues. Schur's Conjecture.'' §F5 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 244-245, 1994. Riesel, H. ``Jacobi's Symbol.'' Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 281-284, 1994. |
![]() for each of the Prime factors
for each of the Prime factors ![]() such that
such that![]() , denoted
, denoted ![]() . When
. When ![]() is a Prime, the Jacobi symbol reduces to the Legendre Symbol. TheJacobi symbol satisfies the same rules as the Legendre Symbol
is a Prime, the Jacobi symbol reduces to the Legendre Symbol. TheJacobi symbol satisfies the same rules as the Legendre Symbol![]() .
.