| 释义 |
Jacobi Triple ProductThe Jacobi triple product is the beautiful identity
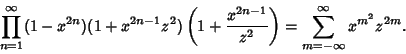 | (1) |
 | (2) |
 , (1) becomes , (1) becomes
where  is the one-variable Ramanujan Theta Function. is the one-variable Ramanujan Theta Function.
To prove the identity, define the function
Then
 | (5) |
 (4), (4),
which yields the fundamental relation
 | (7) |
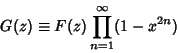 | (8) |
 | (9) |
 | (10) |
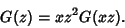 | (11) |
 in a Laurent Series. Since in a Laurent Series. Since  is an Even Function, the Laurent Series contains only even terms. is an Even Function, the Laurent Series contains only even terms.
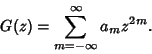 | (12) |
This can be re-indexed with  on the left side of (13) on the left side of (13)
 | (14) |
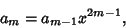 | (15) |
The exponent grows greater by 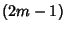 for each increase in for each increase in 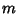 of 1. It is given by of 1. It is given by
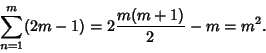 | (19) |
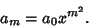 | (20) |
 | (21) |
 must be determined by going back to (4) and (8) and letting must be determined by going back to (4) and (8) and letting  . Then . Then
since multiplication is Associative. It is clear from this expression that the  term must be 1, because allother terms will contain higher Powers of term must be 1, because allother terms will contain higher Powers of 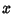 . Therefore, . Therefore,
 | (24) |
See also Euler Identity, Jacobi Identities, Q-Function, Quintuple Product Identity,Ramanujan Psi Sum, Ramanujan Theta Functions, Schröter's Formula, ThetaFunction
References
Andrews, G. E.  -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 63-64, 1986. -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.Borwein, J. M. and Borwein, P. B. ``Jacobi's Triple Product and Some Number Theoretic Applications.'' Ch. 3 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 62-101, 1987. Jacobi, C. G. J. Fundamentia Nova Theoriae Functionum Ellipticarum. Regiomonti, Sumtibus fratrum Borntraeger, p. 90, 1829. Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, p. 470, 1990. |
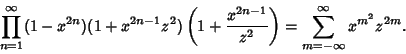
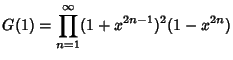
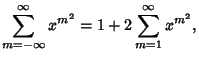
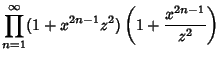

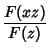


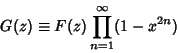


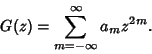




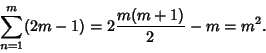

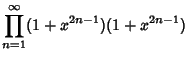



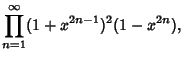

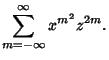
![]() -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.
-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.