Johnson Solid

The Johnson solids are the Convex Polyhedra having regular faces (with the exception of thecompletely regular Platonic Solids, the ``Semiregular''Archimedean Solids, and the two infinite families of Prisms andAntiprisms). There are 28 simple (i.e., cannot be dissected into two otherregular-faced polyhedra by a plane) regular-faced polyhedra in addition to the Prisms andAntiprisms (Zalgaller 1969), and Johnson (1966) proposed and Zalgaller (1969) proved that thereexist exactly 92 Johnson solids in all.

A database of solids and Vertex Nets of these solids is maintainedon the Bell Laboratories Netlib server, but a few errors exist inseveral entries. A concatenated and corrected version of the files is given by Weisstein, together with Mathematica (Wolfram Research, Champaign, IL) code to display the solids and nets. The following table summarizesthe names of the Johnson solids and gives their images and nets.

1. Square pyramid

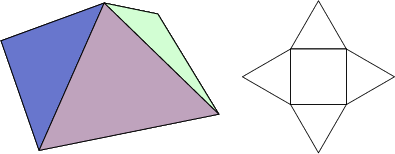
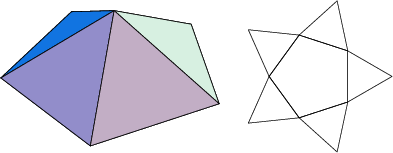
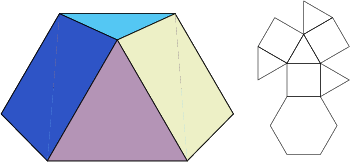
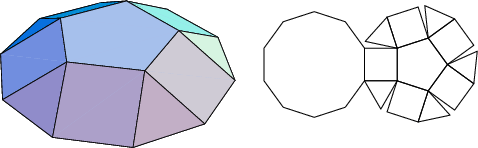
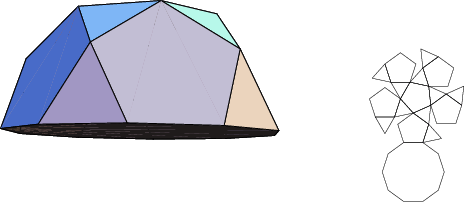
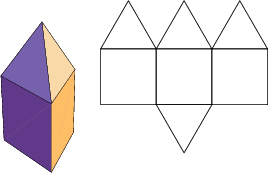
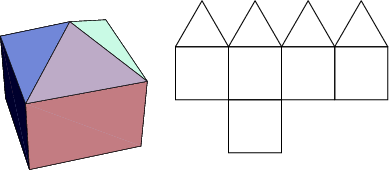
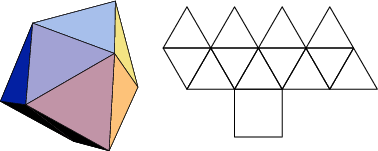
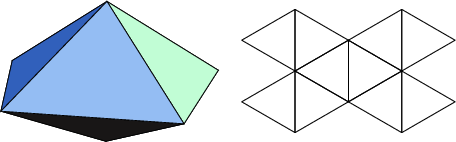
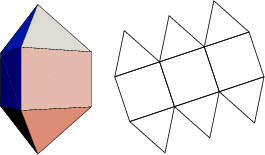
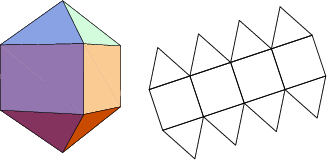
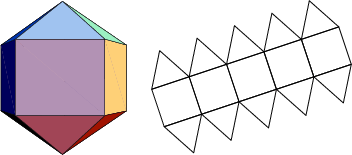
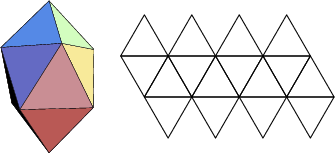
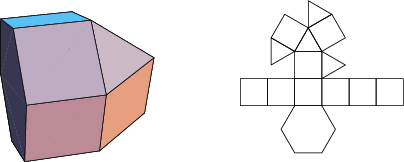
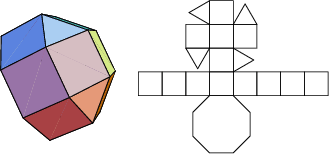
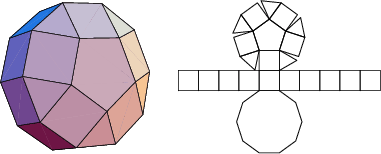
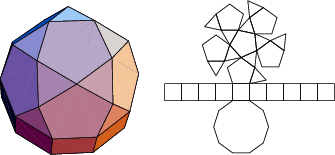
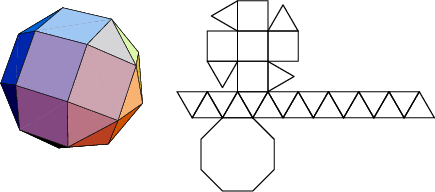
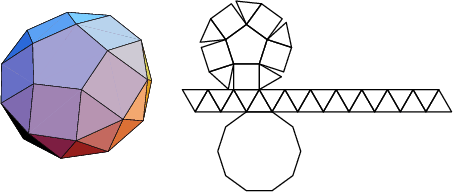
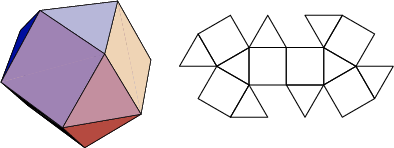
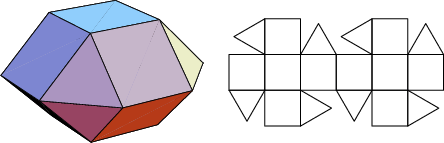
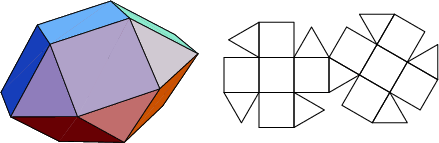
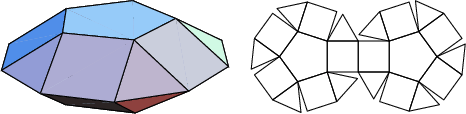
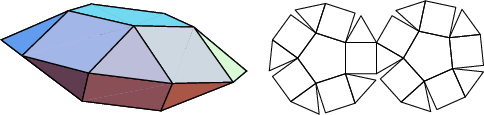
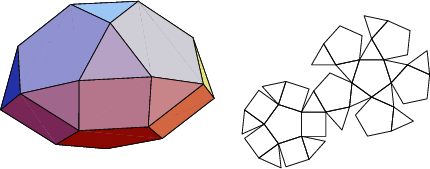
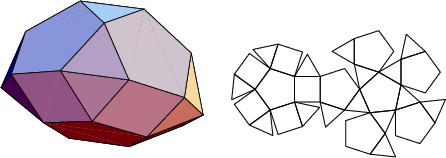
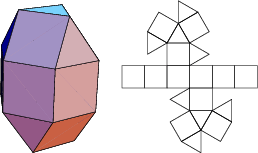
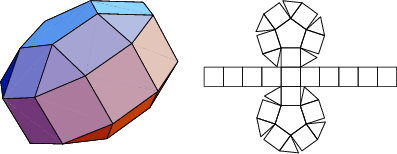
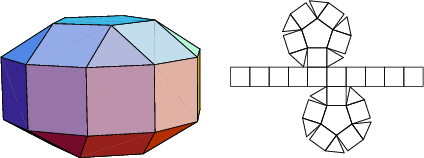
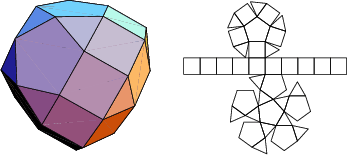
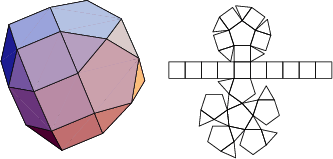
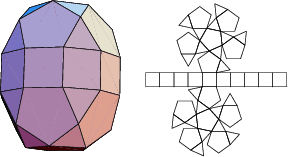
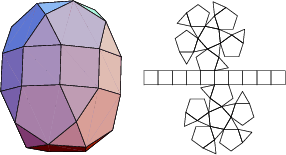
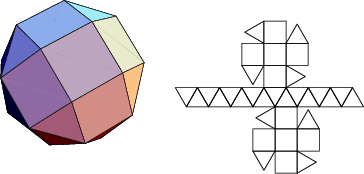
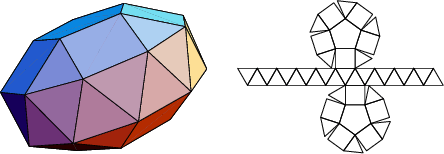
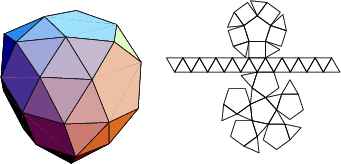
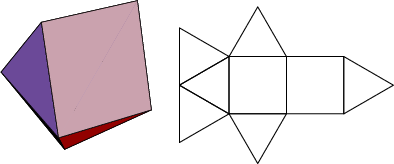
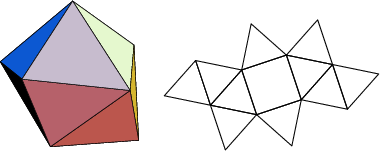
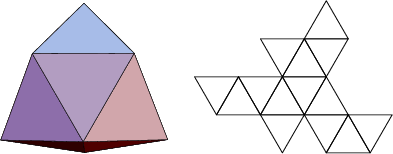
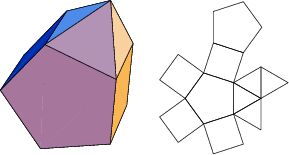
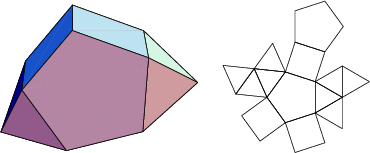
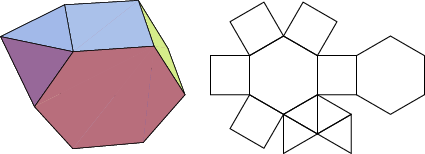
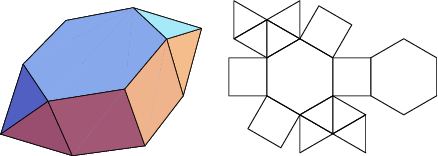
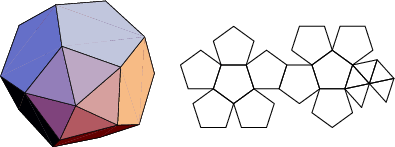
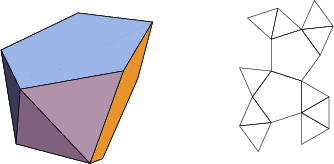
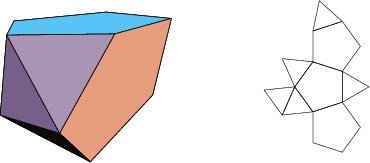
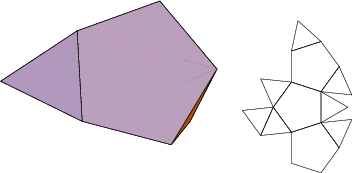
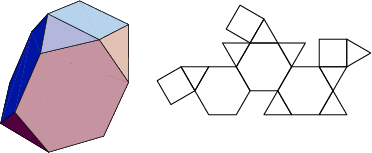
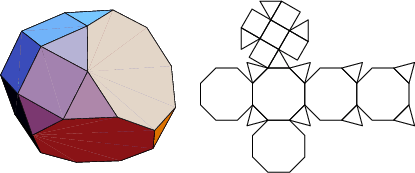
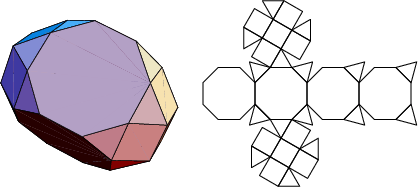
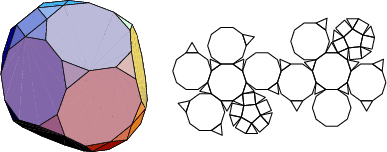
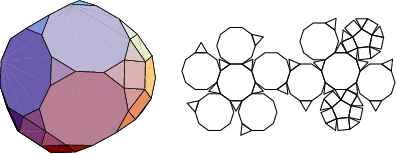
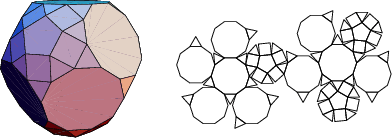
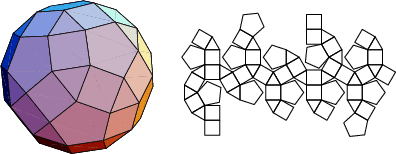
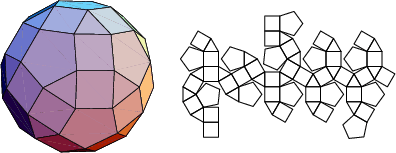
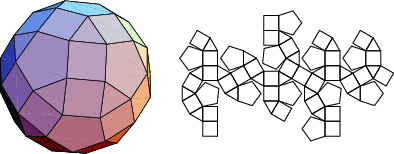
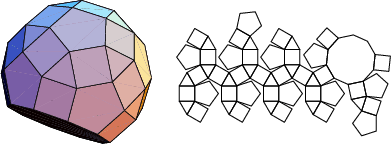
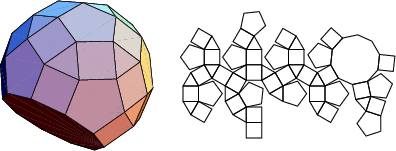
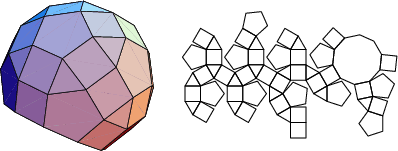
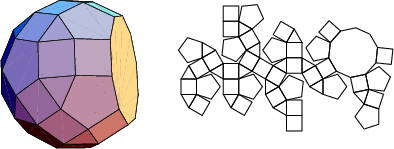
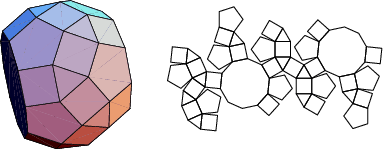
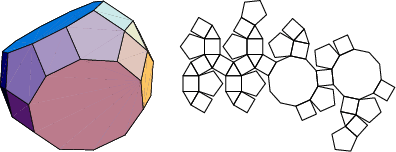
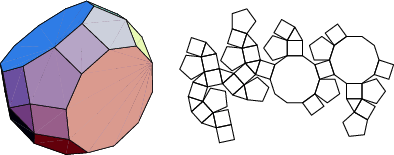
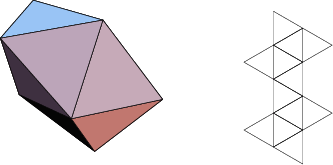
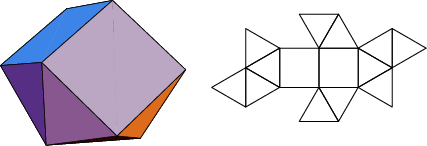
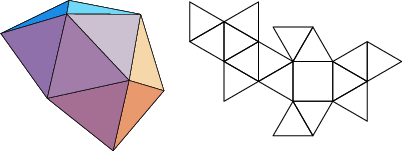
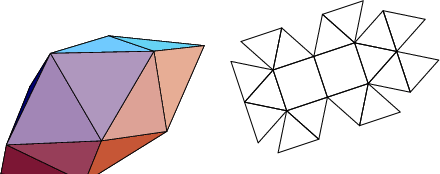
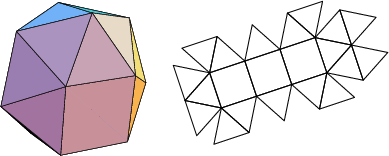
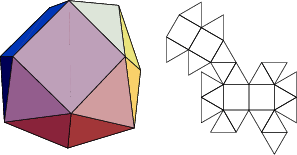
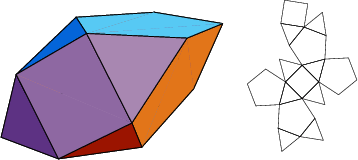
The number of constituent -gons () for each Johnson solid are given in the following table.

1	4	1					47	35	5	7
2	5		1				48	40		12
3	4	3		1			49	6	2
4	4	5			1		50	10	1
5	5	5	1			1	51	14
6	10		6			1	52	4	4	2
7	4	3					53	8	3	2
8	4	5					54	4	5		2
9	5	5	1				55	8	4		2
10	12	1					56	8	4		2
11	15		1				57	12	3		2
12	6						58	5		11
13	10						59	10		10
14	6	3					60	10		10
15	8	4					61	15		9
16	10	5					62	10		2
17	16						63	5		3
18	4	9		1			64	7		3
19	4	13			1		65	8	3		3
20	5	15	1			1	66	12	5			5
21	10	10	6			1	67	16	10			4
22	16	3		1			68	25	5	1			11
23	20	5			1		69	30	10	2			10
24	25	5	1			1	70	30	10	2			10
25	30		6			1	71	35	15	3			9
26	4	4					72	20	30	12
27	8	6					73	20	30	12
28	8	10					74	20	30	12
29	8	10					75	20	30	12
30	10	10	2				76	15	25	11			1
31	10	10	2				77	15	25	11			1
32	15	5	7				78	15	25	11			1
33	15	5	7				79	15	25	11			1
34	20		12				80	10	20	10			2
35	8	12					81	10	20	10			2
36	8	12					82	10	20	10			2
37	8	18					83	5	15	9			3
38	10	20	2				84	12
39	10	20	2				85	24	2
40	15	15	7				86	12	2
41	15	15	7				87	16	1
42	20	10	12				88	16	2
43	20	10	12				89	18	3
44	20	6					90	20	4
45	24	10					91	8	2	4
46	30	10	2				92	13	3	3	1

References

Bell Laboratories. http://netlib.bell-labs.com/netlib/polyhedra/.

Bulatov, V. ``Johnson Solids.'' http://www.physics.orst.edu/~bulatov/polyhedra/johnson/.

Cromwell, P. R. Polyhedra. New York: Cambridge University Press, pp. 86-92, 1997.

Hart, G. W. ``NetLib Polyhedra DataBase.'' http://www.li.net/~george/virtual-polyhedra/netlib-info.html.

Holden, A. Shapes, Space, and Symmetry. New York: Dover, 1991.

Hume, A. Exact Descriptions of Regular and Semi-Regular Polyhedra and Their Duals. Computer Science Technical Report #130. Murray Hill, NJ: AT&T Bell Laboratories, 1986.

Johnson, N. W. ``Convex Polyhedra with Regular Faces.'' Canad. J. Math. 18, 169-200, 1966.

Pugh, A. ``Further Convex Polyhedra with Regular Faces.'' Ch. 3 in Polyhedra: A Visual Approach. Berkeley, CA: University of California Press, pp. 28-35, 1976.

Weisstein, E. W. ``Johnson Solids.'' Mathematica notebook JohnsonSolids.m.

Weisstein, E. W. ``Johnson Solid Netlib Database.'' Mathematica notebook JohnsonSolids.dat.

Zalgaller, V. Convex Polyhedra with Regular Faces. New York: Consultants Bureau, 1969.

• Cross
• Cross-Cap
• Cross-Correlation
• Cross-Correlation Coefficient
• Cross-Correlation Theorem
• Cross Curve
• Crossed Ladders Problem
• Crossed Trough
• Cross Fractal
• Crossing Number (Graph)
• Crossing Number (Link)
• Cross of Lorraine
• Cross Polytope
• Cross Product
• Cross-Ratio
• Cross-Section
• Crout's Method
• Crowd
• Crown
• Crucial Point
• Cruciform
• Crunode
• Cryptarithm
• Cryptarithmetic
• Cryptography