Jordan's Lemma
Jordan's lemma shows the value of the Integral
| (1) |
| (2) |
To derive the lemma, write
| (3) | |||
| (4) |
and define the Contour Integral
| (5) |
 | |||
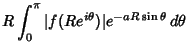 | |||
 | (6) |
Now, if
| (7) |
| (8) |
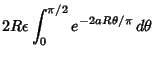 | |||
 | (9) |
As long as
| (10) |
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 406-408, 1985.
- Ideal Number
- Ideal (Partial Order)
- Ideal Point
- Idele
- Idemfactor
- Idempotent
- Identity
- Identity Element
- Identity Function
- Identity Map
- Identity Matrix
- Identity Operator
- Idoneal Number
- Iff
- Ill-Conditioned
- Illumination Problem
- Illusion
- Image
- Imaginary Identity
- Imaginary Number
- Imaginary Part
- Imaginary Point
- Imaginary Quadratic Field
- Immanant
- Immersed Minimal Surface