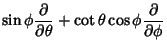| 释义 |
Killing VectorsIf any set of points is displaced by  where all distance relationships are unchanged (i.e., there is an Isometry), then the Vector field is called a Killing vector. where all distance relationships are unchanged (i.e., there is an Isometry), then the Vector field is called a Killing vector.
 | (1) |
 | (2) |
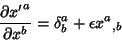 | (3) |
where  is the Lie Derivative. An ordinary derivative can be replaced with a covariant derivative in aLie Derivative, so we can take as the definition is the Lie Derivative. An ordinary derivative can be replaced with a covariant derivative in aLie Derivative, so we can take as the definition
 | (5) |
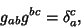 | (6) |
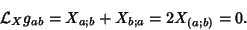 | (7) |
 satisfies satisfies
 | (8) |
 | (9) |
 | (10) |
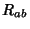 is the Ricci Tensor and is the Ricci Tensor and  is the Riemann Tensor. is the Riemann Tensor.
A 2-sphere with Metric
 | (11) |

The Killing vectors in Euclidean 3-space are
In Minkowski Space, there are 10 Killing vectors
The first group is Translation, the second Rotation, and the final corresponds to a ``boost  .'' .''
|
![]() where all distance relationships are unchanged (i.e., there is an Isometry), then the Vector field is called a Killing vector.
where all distance relationships are unchanged (i.e., there is an Isometry), then the Vector field is called a Killing vector.