Perrin Pseudoprime
If 
is Prime, then 
, where 
is a member of the Perrin Sequence 0, 2, 3, 2, 5, 5, 7, 10, 12, 17,... (Sloane's A001608). A Perrin pseudoprime is a Composite Number 
such that 
. Several``unrestricted'' Perrin pseudoprimes are known, the smallest of which are 271441, 904631, 16532714, 24658561, ...(Sloane's A013998).
Adams and Shanks (1982) discovered the smallest unrestricted Perrin pseudoprime after unsuccessful searches by Perrin (1899),Malo (1900), Escot (1901), and Jarden (1966). (Stewart's 1996 article stating no Perrin pseudoprimes were known was in error.)
Grantham (1996) generalized the definition of Perrin pseudoprime with parameters 
to be an Odd CompositeNumber for which either
- 1.
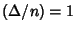and 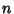has an S-Signature, or - 2.
and 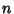has a Q-Signature,
is the Jacobi Symbol. All the 55 Perrin pseudoprimes less than 
have been computed by Kurtz et al. (1986). All have S-Signature, and form the sequence Sloane calls ``restricted'' Perrin pseudoprimes:27664033, 46672291, 102690901, ... (Sloane's A018187). See also Perrin Sequence, Pseudoprime
References
Adams, W. W. ``Characterizing Pseudoprimes for Third-Order Linear Recurrence Sequences.'' Math Comput. 48, 1-15, 1987. Adams, W. and Shanks, D. ``Strong Primality Tests that Are Not Sufficient.'' Math. Comput. 39, 255-300, 1982. Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, p. 305, 1996. Escot, E.-B. ``Solution to Item 1484.'' L'Intermédiare des Math. 8, 63-64, 1901. Grantham, J. ``Frobenius Pseudoprimes.'' http://www.clark.net/pub/grantham/pseudo/pseudo1.ps Holzbaur, C. ``Perrin Pseudoprimes.'' http://ftp.ai.univie.ac.at/perrin.html. Jarden, D. Recurring Sequences. Jerusalem: Riveon Lematematika, 1966. Kurtz, G. C.; Shanks, D.; and Williams, H. C. ``Fast Primality Tests for Numbers Less than Perrin, R. ``Item 1484.'' L'Intermédiare des Math. 6, 76-77, 1899. Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, p. 135, 1996. Sloane, N. J. A.A013998,A018187, andA001608/M0429in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Stewart, I. ``Tales of a Neglected Number.'' Sci. Amer. 274, 102-103, June 1996.
.'' Math. Comput. 46, 691-701, 1986.
- Fisher Index
- Fisher Kurtosis
- Fisher's Block Design Inequality
- Fisher's Estimator Inequality
- Fisher's Exact Test
- Fisher Sign Test
- Fisher Skewness
- Fisher's Theorem
- Fisher's z-Distribution
- Fisher's z'-Transformation
- Fisher-Tippett Distribution
- Fitting Subgroup
- Five Cubes
- Five Disks Problem
- Five Tetrahedra Compound
- Fixed
- Fixed Element
- Fixed Point
- Fixed Point (Differential Equations)
- Fixed Point (Map)
- Fixed Point Theorem
- Fixed Point (Transformation)
- Flag
- Flag Manifold
- Flat