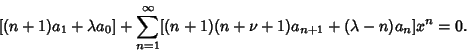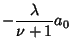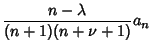| 释义 |
Laguerre Differential Equation
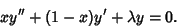 | (1) |
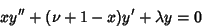 | (2) |
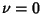 . Note that if . Note that if  , then the solution to the associated Laguerre differential equation is of theform , then the solution to the associated Laguerre differential equation is of theform
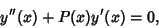 | (3) |
so
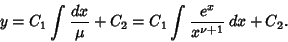 | (5) |
The associated Laguerre differential equation has a Regular Singular Point at 0 and an IrregularSingularity at  . It can be solved using a series expansion, . It can be solved using a series expansion, 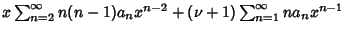 | | 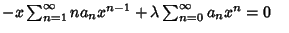 | (6) |
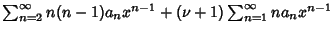 | |  | (7) |
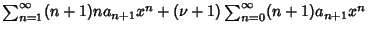 | |  | (8) |
 | (9) |
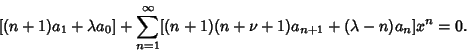 | (10) |
for 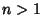 . Therefore, . Therefore,
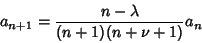 | (13) |
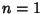 , 2, ..., so , 2, ..., so
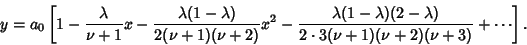 | (14) |
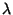 is a Positive Integer, then the series terminates and the solution is a Polynomial, knownas an associated Laguerre Polynomial (or, if is a Positive Integer, then the series terminates and the solution is a Polynomial, knownas an associated Laguerre Polynomial (or, if 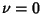 , simply aLaguerre Polynomial).See also Laguerre Polynomial , simply aLaguerre Polynomial).See also Laguerre Polynomial
|
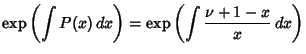
![]() . It can be solved using a series expansion,
. It can be solved using a series expansion,