| 释义 |
Laguerre PolynomialSolutions to the Laguerre Differential Equation with 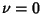 are called Laguerre polynomials. The Laguerrepolynomials are called Laguerre polynomials. The Laguerrepolynomials  are illustrated above for are illustrated above for  and and 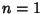 , 2, ..., 5. , 2, ..., 5.
The Rodrigues formula for the Laguerre polynomials is
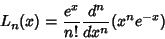 | (1) |
A Contour Integral is given by
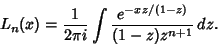 | (3) |
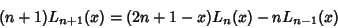 | (4) |
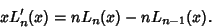 | (5) |
Solutions to the associated Laguerre Differential Equation with  are called associated Laguerrepolynomials are called associated Laguerrepolynomials 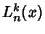 . In terms of the normal Laguerre polynomials, . In terms of the normal Laguerre polynomials,
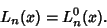 | (6) |
and the Generating Function is
 | (9) |
 with respect to the Weighting Function with respect to the Weighting Function 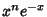 . .
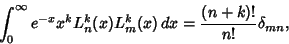 | (10) |
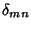 is the Kronecker Delta. They also satisfy is the Kronecker Delta. They also satisfy
 | (11) |
Recurrence Relations include
 | (12) |
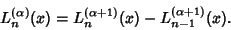 | (13) |
In terms of the Confluent Hypergeometric Function,
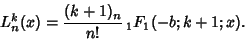 | (15) |
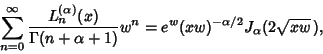 | (16) |
 is the Gamma Function and is the Gamma Function and 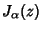 is the Bessel Function of the First Kind (Szegö1975, p. 102). An integral representation is is the Bessel Function of the First Kind (Szegö1975, p. 102). An integral representation is
 | (17) |
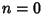 , 1, ...and , 1, ...and 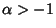 . The Discriminant is . The Discriminant is
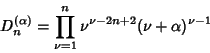 | (18) |
 | (19) |
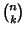 is a Binomial Coefficient (Szegö 1975, p. 101). is a Binomial Coefficient (Szegö 1975, p. 101).
The first few associated Laguerre polynomials are
See also Sonine Polynomial
ReferencesAbramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.Arfken, G. ``Laguerre Functions.'' §13.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 721-731, 1985. Chebyshev, P. L. ``Sur le développement des fonctions à une seule variable.'' Bull. Ph.-Math., Acad. Imp. Sc. St. Pétersbourg 1, 193-200, 1859. Chebyshev, P. L. Oeuvres, Vol. 1. New York: Chelsea, pp. 499-508, 1987. Iyanaga, S. and Kawada, Y. (Eds.). ``Laguerre Functions.'' Appendix A, Table 20.VI in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1481, 1980. Laguerre, E. de. ``Sur l'intégrale  .'' Bull. Soc. math. France 7, 72-81, 1879. Reprinted in Oeuvres, Vol. 1. New York: Chelsea, pp. 428-437, 1971. .'' Bull. Soc. math. France 7, 72-81, 1879. Reprinted in Oeuvres, Vol. 1. New York: Chelsea, pp. 428-437, 1971. Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, pp. 61-62, 1996. Sansone, G. ``Expansions in Laguerre and Hermite Series.'' Ch. 4 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 295-385, 1991. Spanier, J. and Oldham, K. B. ``The Laguerre Polynomials  .'' Ch. 23 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 209-216, 1987. .'' Ch. 23 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 209-216, 1987. Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
|

![]() are called Laguerre polynomials. The Laguerrepolynomials
are called Laguerre polynomials. The Laguerrepolynomials ![]() are illustrated above for
are illustrated above for ![]() and
and ![]() , 2, ..., 5.
, 2, ..., 5.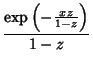
![]() are called associated Laguerrepolynomials
are called associated Laguerrepolynomials ![]() . In terms of the normal Laguerre polynomials,
. In terms of the normal Laguerre polynomials,






![]() .'' Bull. Soc. math. France 7, 72-81, 1879. Reprinted in Oeuvres, Vol. 1. New York: Chelsea, pp. 428-437, 1971.
.'' Bull. Soc. math. France 7, 72-81, 1879. Reprinted in Oeuvres, Vol. 1. New York: Chelsea, pp. 428-437, 1971.![]() .'' Ch. 23 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 209-216, 1987.
.'' Ch. 23 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 209-216, 1987.