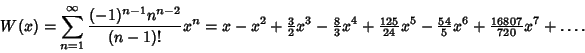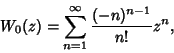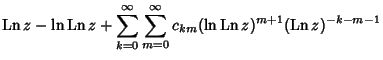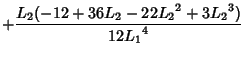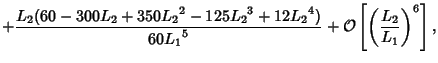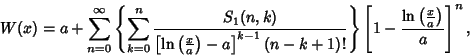| 释义 |
Lambert's W-FunctionThe inverse of the function
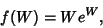 | (1) |
 (WolframResearch, Champaign, IL) function ProductLog[z]. (WolframResearch, Champaign, IL) function ProductLog[z]. 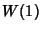 is called the Omega Constant and can be considered asort of ``Golden Ratio'' of exponentials since is called the Omega Constant and can be considered asort of ``Golden Ratio'' of exponentials since
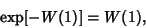 | (2) |
 | (3) |
Lambert's 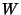 -Function has the series expansion -Function has the series expansion
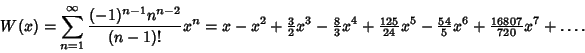 | (4) |
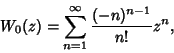 | (5) |
 is a Factorial. However, this series oscillates between ever larger Positive and Negative valuesfor Real is a Factorial. However, this series oscillates between ever larger Positive and Negative valuesfor Real 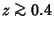 , and so cannot be used for practical numerical computation. An asymptoticFormula which yields reasonably accurate results for , and so cannot be used for practical numerical computation. An asymptoticFormula which yields reasonably accurate results for  is is
where
(Corless et al.), correcting a typographical error in de Bruijn (1961). Another expansion due to Gosper is theDouble Sum
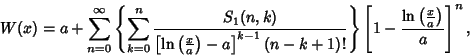 | (9) |
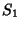 is a nonnegative Stirling Number of the First Kind and is a nonnegative Stirling Number of the First Kind and 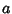 is a first approximation which can beused to select between branches. Lambert's is a first approximation which can beused to select between branches. Lambert's 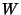 -function is two-valued for -function is two-valued for 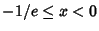 . For . For  , the function isdenoted , the function isdenoted  or simply or simply  , and this is called the principal branch. For , and this is called the principal branch. For 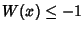 , the function is denoted , the function is denoted . The Derivative of . The Derivative of 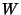 is is
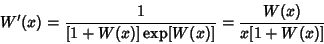 | (10) |
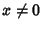 . For the principal branch when . For the principal branch when  , ,
 | (11) |
References
de Bruijn, N. G. Asymptotic Methods in Analysis. Amsterdam, Netherlands: North-Holland, pp. 27-28, 1961.
|
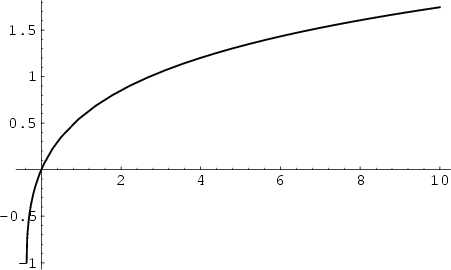
![]() -Function has the series expansion
-Function has the series expansion