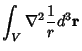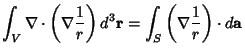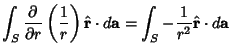| 释义 |
LaplacianThe Laplacian operator for a Scalar function 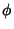 is defined by is defined by
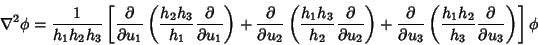 | (1) |
 are the Scale Factorsof the coordinate system. In Tensor notation, the Laplacian is written are the Scale Factorsof the coordinate system. In Tensor notation, the Laplacian is written
where  is a Covariant Derivative and is a Covariant Derivative and
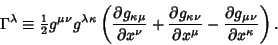 | (3) |
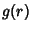 , ,
Using the Vector Derivative identity
 | (6) |
Therefore, for a radial Power law,
A Vector Laplacian can also be defined for a Vector A by
 | (9) |
 , and the identity becomes , and the identity becomes
Similarly, a Tensor Laplacian can be given by
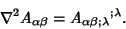 | (11) |
An identity satisfied by the Laplacian is
 | (12) |
 is the Hilbert-Schmidt Norm, is the Hilbert-Schmidt Norm,  is a row Vector, and is a row Vector, and  is theMatrix Transpose of A. is theMatrix Transpose of A.
To compute the Laplacian of the inverse distance function  , where , where  , and integrate theLaplacian over a volume, , and integrate theLaplacian over a volume,
 | (13) |
where the integration is over a small Sphere of Radius 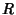 . Now, for . Now, for 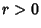 and and 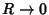 , the integralbecomes 0. Similarly, for , the integralbecomes 0. Similarly, for 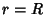 and and 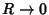 , the integral becomes , the integral becomes 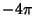 . Therefore, . Therefore,
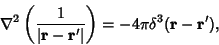 | (15) |
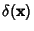 is the Delta Function.See also Antilaplacian is the Delta Function.See also Antilaplacian
|
![]() is defined by
is defined by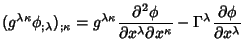
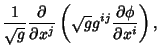

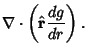
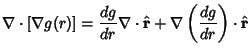

![]() , where
, where ![]() , and integrate theLaplacian over a volume,
, and integrate theLaplacian over a volume,