| 释义 |
Legendre-Gauss QuadratureAlso called ``the'' Gaussian Quadrature or Legendre Quadrature. A Gaussian Quadrature over theinterval 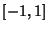 with Weighting Function with Weighting Function 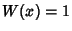 . The Abscissas for quadrature order . The Abscissas for quadrature order 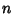 aregiven by the roots of the Legendre Polynomials aregiven by the roots of the Legendre Polynomials 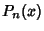 , which occur symmetrically about 0.The weights are , which occur symmetrically about 0.The weights are
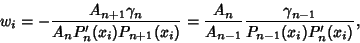 | (1) |
 is the Coefficient of is the Coefficient of  in in 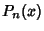 . For Legendre Polynomials, . For Legendre Polynomials,
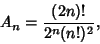 | (2) |
Additionally,
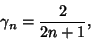 | (4) |
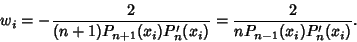 | (5) |
 | (6) |
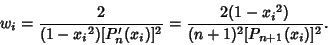 | (7) |
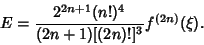 | (8) |
 , and Chandrasekhar (1960) up to , and Chandrasekhar (1960) up to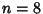 for for 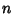 Even. Even.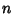 | 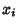 |  | | 2 | ± 0.57735 | 1.000000 | | 3 | 0 | 0.888889 | | | ± 0.774597 | 0.555556 | | 4 | ± 0.339981 | 0.652145 | | | ± 0.861136 | 0.347855 | | 5 | 0 | 0.568889 | | | ± 0.538469 | 0.478629 | | | ± 0.90618 | 0.236927 |
The Abscissas and weights can be computed analytically for small 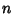 . .
ReferencesBeyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 462-463, 1987.Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 56-62, 1960. Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 323-325, 1956.
|
![]() with Weighting Function
with Weighting Function ![]() . The Abscissas for quadrature order
. The Abscissas for quadrature order ![]() aregiven by the roots of the Legendre Polynomials
aregiven by the roots of the Legendre Polynomials ![]() , which occur symmetrically about 0.The weights are
, which occur symmetrically about 0.The weights are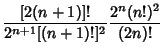

![]() .
.