| 释义 |
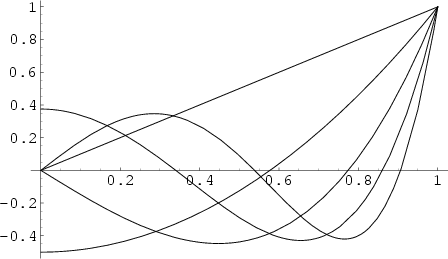
Legendre PolynomialThe Legendre Functions of the First Kind are solutions to theLegendre Differential Equation. If  is an Integer, they are Polynomials. Theyare a special case of the Ultraspherical Functions with is an Integer, they are Polynomials. Theyare a special case of the Ultraspherical Functions with  . The Legendrepolynomials . The Legendrepolynomials 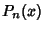 are illustrated above for are illustrated above for 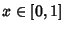 and and 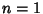 , 2, ..., 5. , 2, ..., 5.
The Rodrigues Formula provides the Generating Function
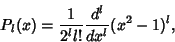 | (1) |
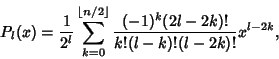 | (2) |
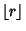 is the Floor Function. The Generating Function is is the Floor Function. The Generating Function is
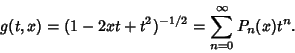 | (3) |
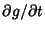 , ,
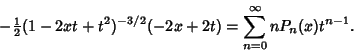 | (4) |
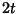 , ,
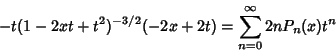 | (5) |
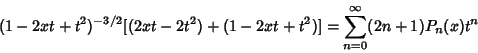 | (6) |
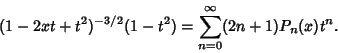 | (7) |
 and computing the charge distribution on a Sphere. They satisfy theRecurrence Relation and computing the charge distribution on a Sphere. They satisfy theRecurrence Relation
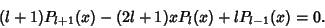 | (8) |
The Legendre polynomials are orthogonal over 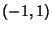 with Weighting Function 1 and satisfy with Weighting Function 1 and satisfy
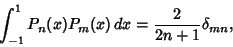 | (9) |
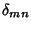 is the Kronecker Delta. is the Kronecker Delta.
A Complex Generating Function is
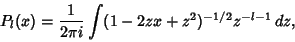 | (10) |
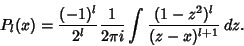 | (11) |
Additional integrals (Byerly 1959, p. 172) include
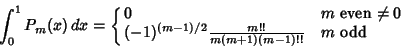 | (12) |
 | (13) |
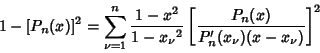 | (14) |
The first few Legendre polynomials are
The first few Powers in terms of Legendre polynomials are
For Legendre polynomials and Powers up to exponent 12, see Abramowitz and Stegun (1972, p. 798).
The Legendre Polynomials can also be generated using Gram-Schmidt Orthonormalization in theOpen Interval 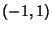 with the Weighting Function 1. with the Weighting Function 1.
Normalizing so that  gives the expected Legendre polynomials. gives the expected Legendre polynomials.
The ``shifted'' Legendre polynomials are a set of functions analogous to the Legendre polynomials, but defined on theinterval (0, 1). They obey the Orthogonality relationship
 | (19) |
The associated Legendre polynomials 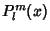 are solutions to the associated Legendre Differential Equation,where are solutions to the associated Legendre Differential Equation,where  is a Positive Integer and is a Positive Integer and  , ..., , ...,  . They can be given in terms of the unassociated polynomials by . They can be given in terms of the unassociated polynomials by
where 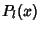 are the unassociated Legendre Polynomials. Note that some authors (e.g.,Arfken 1985, p. 668) omit the Condon-Shortley Phase are the unassociated Legendre Polynomials. Note that some authors (e.g.,Arfken 1985, p. 668) omit the Condon-Shortley Phase 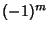 , while others include it (e.g., Abramowitz and Stegun1972, Press et al. 1992, and the LegendreP[l,m,z] command of Mathematica , while others include it (e.g., Abramowitz and Stegun1972, Press et al. 1992, and the LegendreP[l,m,z] command of Mathematica ). Abramowitz and Stegun(1972, p. 332) use the notation ). Abramowitz and Stegun(1972, p. 332) use the notation
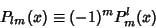 | (21) |
Associated polynomials are sometimes called Ferrers' Functions(Sansone 1991, p. 246). If  , they reduce to the unassociated Polynomials. The associatedLegendre functions are part of the Spherical Harmonics, which are the solution ofLaplace's Equation in Spherical Coordinates. They are Orthogonal over , they reduce to the unassociated Polynomials. The associatedLegendre functions are part of the Spherical Harmonics, which are the solution ofLaplace's Equation in Spherical Coordinates. They are Orthogonal over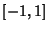 with the Weighting Function 1 with the Weighting Function 1
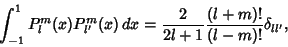 | (22) |
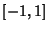 with respect to with respect to 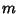 with the Weighting Function with the Weighting Function 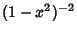
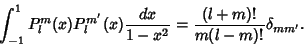 | (23) |
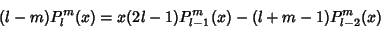 | (24) |
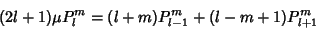 | (26) |
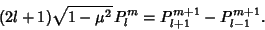 | (27) |
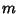 to the corresponding functions with Positive to the corresponding functions with Positive 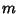 is is
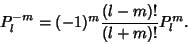 | (28) |
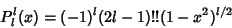 | (29) |
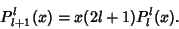 | (30) |
 and using the convention without a leading factor of and using the convention without a leading factor of 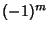 (Arfken 1985, p. 669), the first few associated Legendre polynomials are (Arfken 1985, p. 669), the first few associated Legendre polynomials are
Written in terms  , the first few become , the first few become
The derivative about the origin is
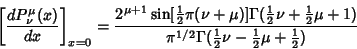 | (31) |
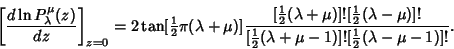 | (32) |
ReferencesAbramowitz, M. and Stegun, C. A. (Eds.). ``Legendre Functions'' and ``Orthogonal Polynomials.'' Ch. 22 in Chs. 8 and 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 331-339 and 771-802, 1972.Arfken, G. ``Legendre Functions.'' Ch. 12 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 637-711, 1985. Binney, J. and Tremaine, S. ``Associated Legendre Functions.'' Appendix 5 in Galactic Dynamics. Princeton, NJ: Princeton University Press, pp. 654-655, 1987. Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959. Iyanaga, S. and Kawada, Y. (Eds.). ``Legendre Function'' and ``Associated Legendre Function.'' Appendix A, Tables 18.II and 18.III in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1462-1468, 1980. Legendre, A. M. ``Sur l'attraction des Sphéroides.'' Mém. Math. et Phys. présentés à l'Ac. r. des. sc. par divers savants 10, 1785. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 593-597, 1953. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 252, 1992. Sansone, G. ``Expansions in Series of Legendre Polynomials and Spherical Harmonics.'' Ch. 3 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 169-294, 1991. Snow, C. Hypergeometric and Legendre Functions with Applications to Integral Equations of Potential Theory. Washington, DC: U. S. Government Printing Office, 1952. Spanier, J. and Oldham, K. B. ``The Legendre Polynomials 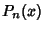 '' and ``The Legendre Functions '' and ``The Legendre Functions  and and 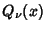 .'' Chs. 21 and 59 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 183-192 and 581-597, 1987. .'' Chs. 21 and 59 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 183-192 and 581-597, 1987. Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
|
![]() is an Integer, they are Polynomials. Theyare a special case of the Ultraspherical Functions with
is an Integer, they are Polynomials. Theyare a special case of the Ultraspherical Functions with ![]() . The Legendrepolynomials
. The Legendrepolynomials ![]() are illustrated above for
are illustrated above for ![]() and
and ![]() , 2, ..., 5.
, 2, ..., 5.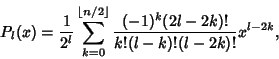
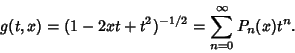
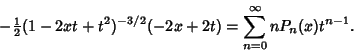
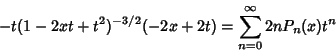
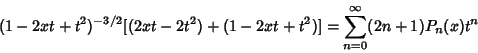
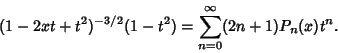
![]() with Weighting Function 1 and satisfy
with Weighting Function 1 and satisfy
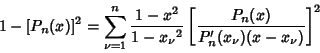
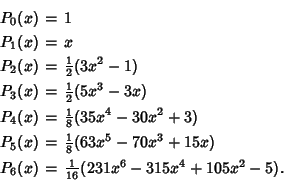
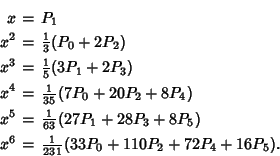
![]() with the Weighting Function 1.
with the Weighting Function 1.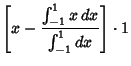
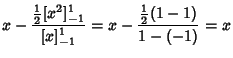
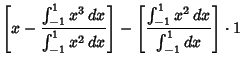
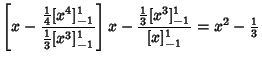
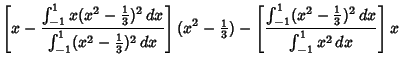
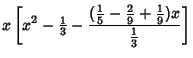
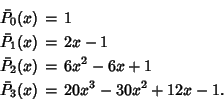
![]() are solutions to the associated Legendre Differential Equation,where
are solutions to the associated Legendre Differential Equation,where ![]() is a Positive Integer and
is a Positive Integer and ![]() , ...,
, ..., ![]() . They can be given in terms of the unassociated polynomials by
. They can be given in terms of the unassociated polynomials by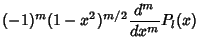
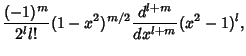
![]() , they reduce to the unassociated Polynomials. The associatedLegendre functions are part of the Spherical Harmonics, which are the solution ofLaplace's Equation in Spherical Coordinates. They are Orthogonal over
, they reduce to the unassociated Polynomials. The associatedLegendre functions are part of the Spherical Harmonics, which are the solution ofLaplace's Equation in Spherical Coordinates. They are Orthogonal over![]() with the Weighting Function 1
with the Weighting Function 1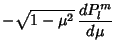
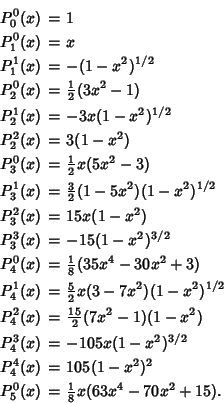
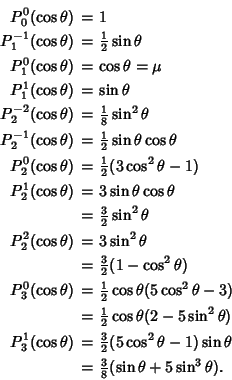
![]() '' and ``The Legendre Functions
'' and ``The Legendre Functions ![]() and
and ![]() .'' Chs. 21 and 59 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 183-192 and 581-597, 1987.
.'' Chs. 21 and 59 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 183-192 and 581-597, 1987.