| 释义 |
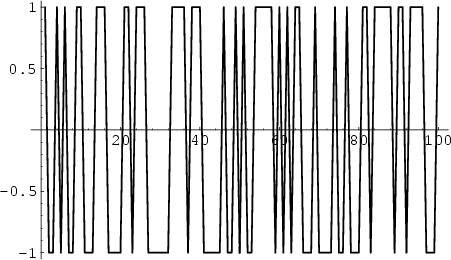
Liouville FunctionThe function
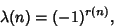 | (1) |
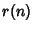 is the number of not necessarily distinct Prime Factors of is the number of not necessarily distinct Prime Factors of  , with , with 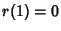 . The first few values of . The first few values of are 1, are 1,  , ,  , 1, , 1,  , 1, , 1,  , ,  , 1, 1, , 1, 1,  , ,  , .... The Liouville function is connected with theRiemann Zeta Function by the equation , .... The Liouville function is connected with theRiemann Zeta Function by the equation
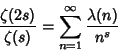 | (2) |
The Conjecture that the Summatory Function
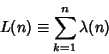 | (3) |
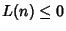 for for 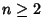 is called the Pólya Conjecture and has been proved to befalse. The first is called the Pólya Conjecture and has been proved to befalse. The first  for which for which 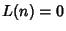 are for are for 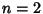 , 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (Sloane's A028488),and , 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (Sloane's A028488),and 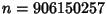 is, in fact, the first counterexample to the Pólya Conjecture (Tanaka1980). However, it is unknown if is, in fact, the first counterexample to the Pólya Conjecture (Tanaka1980). However, it is unknown if 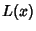 changes sign infinitely often (Tanaka 1980). The first few values of changes sign infinitely often (Tanaka 1980). The first few values of 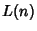 are 1,0, are 1,0,  , 0, , 0,  , 0, , 0,  , ,  , ,  , 0, , 0,  , ,  , , 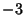 , ,  , ,  , 0, , 0,  , ,  , , 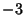 , , 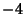 , ... (Sloane's A002819). , ... (Sloane's A002819).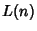 also satisfies also satisfies
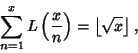 | (4) |
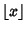 is the Floor Function (Lehman 1960). Lehman (1960) also gives the formulas is the Floor Function (Lehman 1960). Lehman (1960) also gives the formulas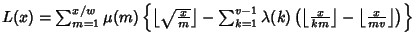 | | 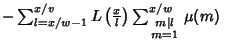 | (5) |
and
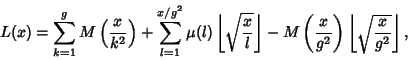 | (6) |
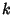 , , 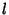 , and , and 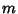 are variables ranging over the Positive integers, are variables ranging over the Positive integers, 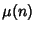 is the MöbiusFunction, is the MöbiusFunction, 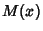 is Mertens Function, and is Mertens Function, and 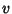 , ,  , and , and  are Positive real numbers with are Positive real numbers with .See also Pólya Conjecture, Prime Factors, Riemann Zeta Function .See also Pólya Conjecture, Prime Factors, Riemann Zeta Function
References
Fawaz, A. Y. ``The Explicit Formula for 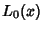 .'' Proc. London Math. Soc. 1, 86-103, 1951. .'' Proc. London Math. Soc. 1, 86-103, 1951.Lehman, R. S. ``On Liouville's Function.'' Math. Comput. 14, 311-320, 1960. Sloane, N. J. A. SequencesA028488 andA002819/M0042in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Tanaka, M. ``A Numerical Investigation on Cumulative Sum of the Liouville Function.'' Tokyo J. Math. 3, 187-189, 1980. |
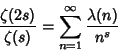

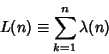
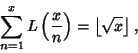
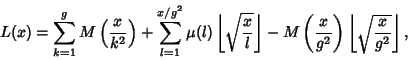
![]() .'' Proc. London Math. Soc. 1, 86-103, 1951.
.'' Proc. London Math. Soc. 1, 86-103, 1951.