“Lobachevsky's Formula”的概念、定义、习题解题方法及翻译-数学辞典

单词

Lobachevsky's Formula

释义

Lobachevsky's Formula

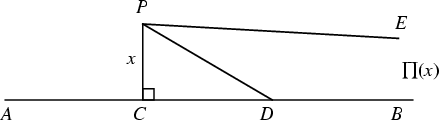
Given a point and a Line , draw the Perpendicular through and call it . Let be any otherline from which meets in . In a Hyperbolic Geometry, as moves off to infinity along , then theline approaches the limiting line , which is said to be parallel to at . The angle which makes with is then called the Angle of Parallelism for perpendicular distance , and is given by

which is called Lobachevsky's formula.

See also Angle of Parallelism, Hyperbolic Geometry

References

Manning, H. P. Introductory Non-Euclidean Geometry. New York: Dover, p. 58, 1963.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。