| 释义 |
Pisot-Vijayaraghavan ConstantsLet  be a number greater than 1, be a number greater than 1, 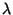 a Positive number, and a Positive number, and
 | (1) |
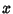 . Then for a given . Then for a given 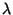 , the sequence of numbers , the sequence of numbers  for for  , 2,... is uniformly distributed in the interval (0, 1) when , 2,... is uniformly distributed in the interval (0, 1) when  does not belong to a does not belong to a 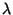 -dependent exceptional set -dependent exceptional set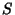 of Measure zero (Koksma 1935). Pisot (1938) and Vijayaraghavan (1941) independently studied the exceptional valuesof of Measure zero (Koksma 1935). Pisot (1938) and Vijayaraghavan (1941) independently studied the exceptional valuesof  , and Salem (1943) proposed calling such values Pisot-Vijayaraghavan numbers. , and Salem (1943) proposed calling such values Pisot-Vijayaraghavan numbers.
Pisot (1938) proved that if  is such that there exists a is such that there exists a  such that the series such that the series  converges, then converges, then  is an Algebraic Integer whose conjugates all (except for itself)have modulus is an Algebraic Integer whose conjugates all (except for itself)have modulus  , and , and 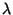 is an algebraic Integer of the Field is an algebraic Integer of the Field 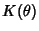 . Vijayaraghavan (1940) provedthat the set of Pisot-Vijayaraghavan numbers has infinitely many limit points. Salem (1944) proved that the set ofPisot-Vijayaraghavan constants is closed. The proof of this theorem is based on the Lemma that for aPisot-Vijayaraghavan constant . Vijayaraghavan (1940) provedthat the set of Pisot-Vijayaraghavan numbers has infinitely many limit points. Salem (1944) proved that the set ofPisot-Vijayaraghavan constants is closed. The proof of this theorem is based on the Lemma that for aPisot-Vijayaraghavan constant  , there always exists a number , there always exists a number 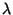 such that such that  and thefollowing inequality is satisfied, and thefollowing inequality is satisfied,
 | (2) |
 of of
 | (3) |
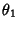 as the root of as the root of
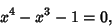 | (4) |
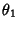 and and 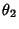 are isolated in are isolated in 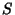 , and showed that the roots of each Polynomial , and showed that the roots of each Polynomial
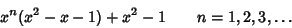 | (5) |
 | (6) |
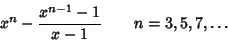 | (7) |
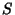 , where , where  (the Golden Mean) is the accumulation point of the set (in fact, the smallest; LeLionnais 1983, p. 40). Some small Pisot-Vijayaraghavan constants and their Polynomials are given in thefollowing table. The latter two entries are from Boyd (1977). (the Golden Mean) is the accumulation point of the set (in fact, the smallest; LeLionnais 1983, p. 40). Some small Pisot-Vijayaraghavan constants and their Polynomials are given in thefollowing table. The latter two entries are from Boyd (1977).
 | number | order | Polynomial | | 0 | 1.3247179572 | 3 | 1 0   | | 1 | 1.3802775691 | 4 | 1  0 0 0 0  | | | 1.6216584885 | 16 | 1 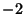 2 2  2 2 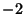 1 0 0 1 1 0 0 1  2 2 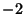 2 2 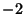 1 1  | | | 1.8374664495 | 20 | 1 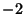 0 1 0 1  0 1 0 1  0 1 0 0 1 0  0 1 0 1  0 1 0 1  0 1 0 1  |
All the points in 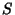 less than less than  are known (Dufresnoy and Pisot 1955). Each point of are known (Dufresnoy and Pisot 1955). Each point of 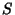 is a limit pointfrom both sides of the set is a limit pointfrom both sides of the set  of Salem Constants (Salem 1945). of Salem Constants (Salem 1945). See also Salem Constants
References
Boyd, D. W. ``Small Salem Numbers.'' Duke Math. J. 44, 315-328, 1977.Dufresnoy, J. and Pisot, C. ``Étude de certaines fonctions méromorphes bornées sur le cercle unité, application à un ensemble fermé d'entiers algébriques.'' Ann. Sci. École Norm. Sup. 72, 69-92, 1955. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 38 and 148, 1983. Koksma, J. F. ``Ein mengentheoretischer Satz über die Gleichverteilung modulo Eins.'' Comp. Math. 2, 250-258, 1935. Pisot, C. ``La répartition modulo 1 et les nombres algébriques.'' Annali di Pisa 7, 205-248, 1938. Salem, R. ``Sets of Uniqueness and Sets of Multiplicity.'' Trans. Amer. Math. Soc. 54, 218-228, 1943. Salem, R. ``A Remarkable Class of Algebraic Numbers. Proof of a Conjecture of Vijayaraghavan.'' Duke Math. J. 11, 103-108, 1944. Salem, R. ``Power Series with Integral Coefficients.'' Duke Math. J. 12, 153-172, 1945. Siegel, C. L. ``Algebraic Numbers whose Conjugates Lie in the Unit Circle.'' Duke Math. J. 11, 597-602, 1944. Vijayaraghavan, T. ``On the Fractional Parts of the Powers of a Number, II.'' Proc. Cambridge Phil. Soc. 37, 349-357, 1941. |
![]() be a number greater than 1,
be a number greater than 1, ![]() a Positive number, and
a Positive number, and ![]() is such that there exists a
is such that there exists a ![]() such that the series
such that the series ![]() converges, then
converges, then ![]() is an Algebraic Integer whose conjugates all (except for itself)have modulus
is an Algebraic Integer whose conjugates all (except for itself)have modulus ![]() , and
, and ![]() is an algebraic Integer of the Field
is an algebraic Integer of the Field ![]() . Vijayaraghavan (1940) provedthat the set of Pisot-Vijayaraghavan numbers has infinitely many limit points. Salem (1944) proved that the set ofPisot-Vijayaraghavan constants is closed. The proof of this theorem is based on the Lemma that for aPisot-Vijayaraghavan constant
. Vijayaraghavan (1940) provedthat the set of Pisot-Vijayaraghavan numbers has infinitely many limit points. Salem (1944) proved that the set ofPisot-Vijayaraghavan constants is closed. The proof of this theorem is based on the Lemma that for aPisot-Vijayaraghavan constant ![]() , there always exists a number
, there always exists a number ![]() such that
such that ![]() and thefollowing inequality is satisfied,
and thefollowing inequality is satisfied,
![]() less than
less than ![]() are known (Dufresnoy and Pisot 1955). Each point of
are known (Dufresnoy and Pisot 1955). Each point of ![]() is a limit pointfrom both sides of the set
is a limit pointfrom both sides of the set ![]() of Salem Constants (Salem 1945).
of Salem Constants (Salem 1945).