| 释义 |
Pochhammer SymbolA.k.a. Rising Factorial. For an Integer 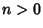 , ,
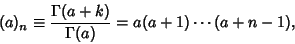 | (1) |
 is the Gamma Function and is the Gamma Function and
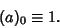 | (2) |
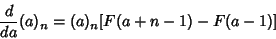 | (3) |
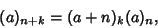 | (4) |
 is the Digamma Function. The Pochhammer symbol arises in series expansions of HypergeometricFunctions and Generalized Hypergeometric Functions.See also Factorial, Generalized Hypergeometric Function, Harmonic Logarithm, Hypergeometric Function is the Digamma Function. The Pochhammer symbol arises in series expansions of HypergeometricFunctions and Generalized Hypergeometric Functions.See also Factorial, Generalized Hypergeometric Function, Harmonic Logarithm, Hypergeometric Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 256, 1972.Spanier, J. and Oldham, K. B. ``The Pochhammer Polynomials 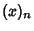 .'' Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987. .'' Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.
|
![]() ,
,![]() .'' Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.
.'' Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.