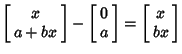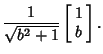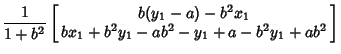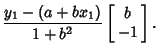| 释义 |
Point-Line Distance--2-DGiven a line  and a point and a point 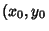 ), in slope-intercept form, the equationof the line is ), in slope-intercept form, the equationof the line is
 | (1) |
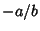 . Points on the line have the vector coordinates . Points on the line have the vector coordinates
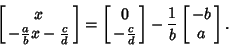 | (2) |
 | (3) |
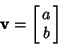 | (4) |
 | (5) |
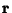 onto onto 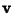 , ,
If the line is represented by the endpoints of a Vector 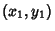 and and 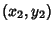 , then the PerpendicularVector is , then the PerpendicularVector is
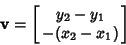 | (7) |
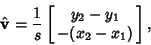 | (8) |
 | (9) |
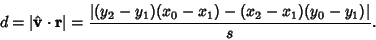 | (10) |
The distance from a point ( , , ) to the line ) to the line 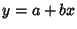 can be computed using Vector algebra. Let can be computed using Vector algebra. Let  be a Vector in the same direction as the line be a Vector in the same direction as the line
A given point on the line is
 | (13) |
Therefore,
 | (15) |
 times the vertical distance times the vertical distance 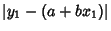 . But the Slope . But the Slope 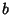 is just is just 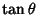 , so , so
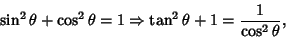 | (16) |
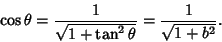 | (17) |
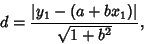 | (18) |
|
![]() and a point
and a point ![]() ), in slope-intercept form, the equationof the line is
), in slope-intercept form, the equationof the line is 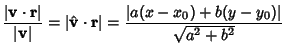
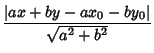

![]() ,
,![]() ) to the line
) to the line ![]() can be computed using Vector algebra. Let
can be computed using Vector algebra. Let ![]() be a Vector in the same direction as the line
be a Vector in the same direction as the line