appeals to intuitive understanding. In general, how-

ever, it is very difficult to explain precisely just what it

is we mean by “space” and the “amount” of it occu-

pied. This is a serious issue. (See Banach-Tarski para-

dox on following page.)

As a starting point, it seems reasonable to say, how-

ever, that a 1 ×1 square should have “area” one. We

call this a basic unit of area. As four of these basic units

fit snugly into a square with side-length two, without

overlap, we say then that a 2 ×2 square has area four.

Similarly a 3 ×3 square has area nine, a 4 ×4 square

area 16, and so on.

A 3 ×6 rectangle holds 18 basic unit squares and

so has area 18. In general, a rectangle that is lunits

long and wunits wide, with both land wwhole num-

bers, has area l×w:

area of a rectangle = length ×width

This is a fundamental formula. To put the notion of

area on a sound footing, we use this formula as a defin-

ing law: the area of any rectangle is to be the product

of its length and its width.

Although it is impossible to fit a whole number of

unit squares into a rectangle that is 5 3/4 units long and

√

—

7 units wide, for example, we declare, nonetheless,

that the area of such a rectangle is the product of these

two numbers. (This agrees with our intuitive idea that,

with the aid of scissors, about 5 3/4 ×√

—

7 ≈15.213 unit

squares will fit in this rectangle.)

From this law, the areas of other geometric shapes

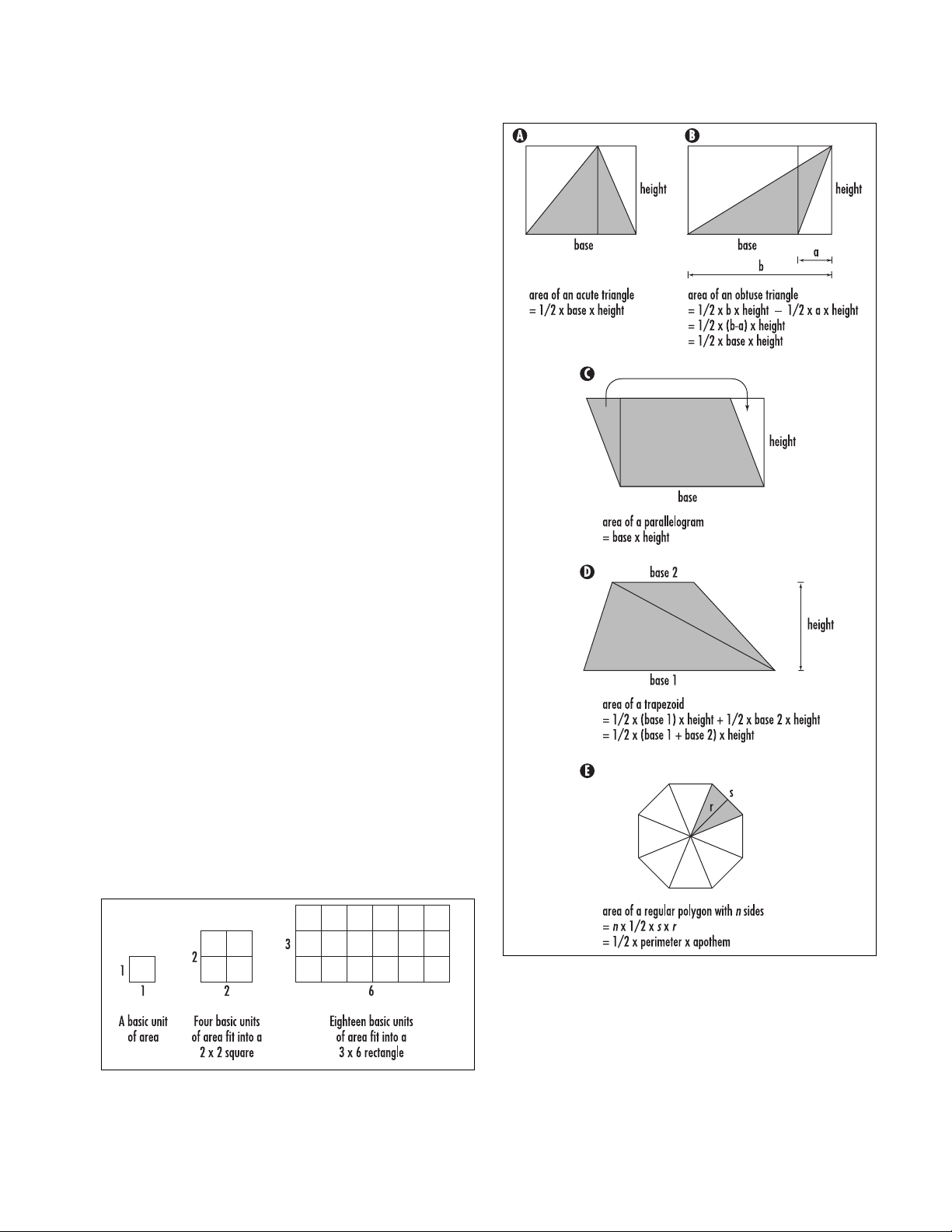
follow. For example, the following diagram shows that

the area of an acute

TRIANGLE

is half the area of the

rectangle that encloses it. This leads to the formula:

area of a triangle = 1/2×base ×height

This formula also holds for obtuse triangles.

By rearranging pieces of a

PARALLELOGRAM

, we see

that its area is given by the formula:

area of a parallelogram = base ×height

area 23

Area

The areas of basic shapes