area = √(s– a)(s– b)(s– c)(s– d)

52 braid

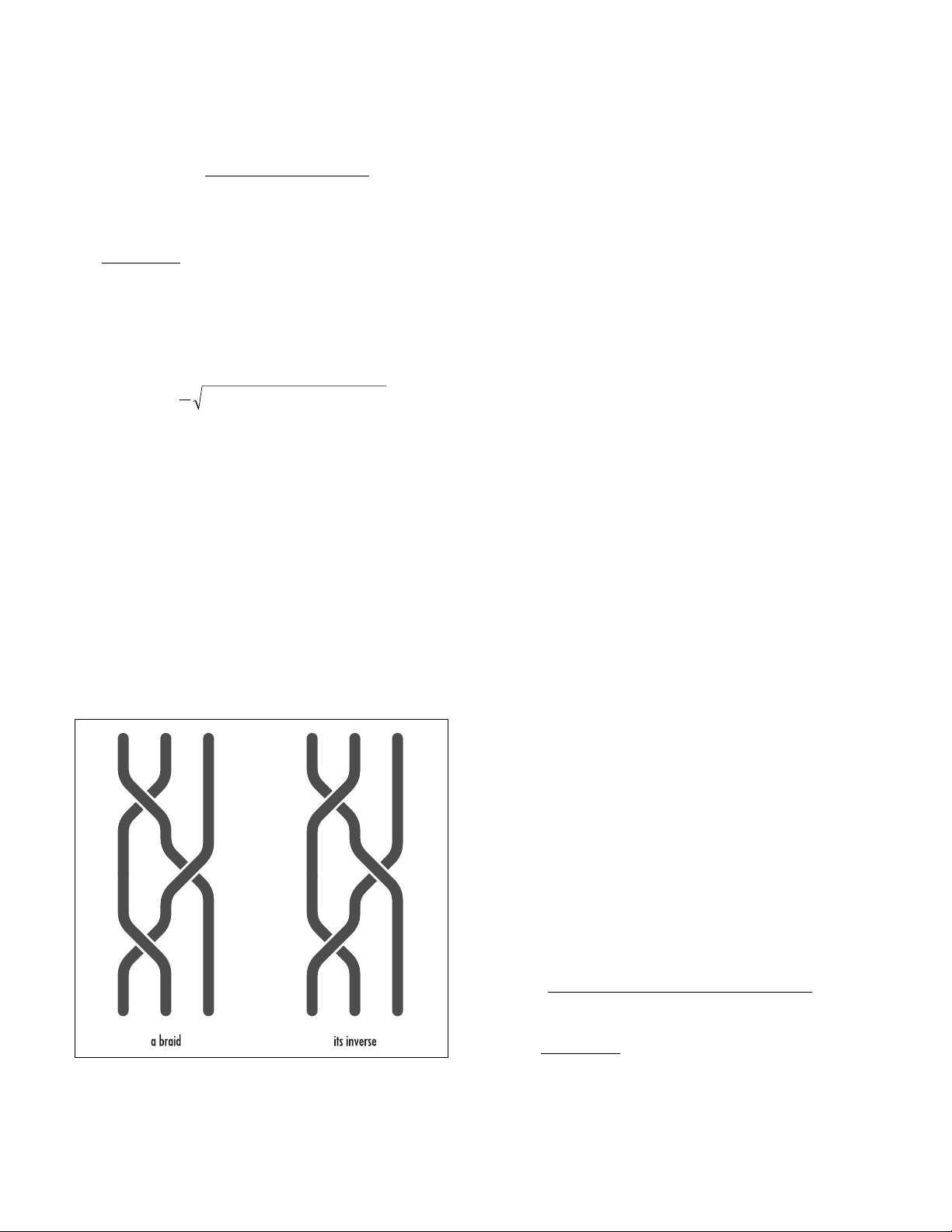
A braid and its inverse

K=

√

(s– a)(s– b)(s– c)(s– d) – abcd cos2(θ)

CIRCLE

solely in terms of the lengths of its four sides.

His formula reads:

where a, b, c, and dare the four side-lengths and

is the figure’s semiperimeter.

If pand qare the lengths of the figure’s two diago-

nals then P

TOLEMY

’

S THEOREM

asserts that pq = ac + bd.

Brahmagupta’s formula follows from B

RETSCHNEIDER

’

S

FORMULA

for the area of a quadrilateral:

by substituting in this value for pq.

If one of the sides of the quadrilateral has length

zero, that is, the figure is a

TRIANGLE

, then Brah-

magupta’s formula reduces to H

ERON

’

S FORMULA

.

See also

CYCLIC POLYGON

.

braid A number of strings plaited together is called a

braid. The theory of braids examines the number of

(essentially distinct) ways a fixed number of strings,

held initially in parallel, can be braided. One can com-

bine two braids on a fixed number of strings by repeat-

ing the pattern of the second braid at the end of the

first braid. If, after completing this maneuver, the act of

physically shaking the system of strings settles the

strands to the unbraided state, then we say that the two

braids are “inverse braids.” For example, the two

braids shown in the diagram are inverse braids.

If a braid consists of nstrings, then the symbol σiis

used to record the act of switching of the ith string over

the (i+ 1)th string (for 1 ≤i≤n– 1) and σi–1 for the act

of switching of the same two strings but in the opposite

sense. A general braid is then described as a string of

these symbols (called a “word”). For instance, the two

braids shown in the diagram below, at left, are repre-

sented by the words σ1σ2–1σ1and σ1–1σ2σ1–1, respec-

tively. A braid with no crossings (that is, in which no

strings cross) is denoted “1,” and the process of combin-

ing braids corresponds precisely to the process of con-

catenating words. Two braids are inverse braids, if, after

performing the suggested symbolic manipulations, their

resulting concatenated word is 1. For instance, in our

example, we have: σ1σ2–1σ1σ1–1σ2σ1–1 = σ1σ2–1σ2σ1–1 =

σ1σ1–1 = 1. It is possible that two different words can

represent the same physical braid. (For instance, on three

strings, the braids σ1σ2σ1and σ2σ1σ2are physically

equivalent.)

Each set of braids on a fixed number of strings

forms a

GROUP

called a braid group. Austrian mathe-

matician Emil Artin (1898–1962) was the first to

study these groups and solve the problem of determin-

ing precisely when two different words represent the

same braid.

Bretschneider’s formula German mathematician

Carl Anton Bretschneider (1808–78) wrote down a for-

mula for the

AREA

of a

QUADRILATERAL

solely in terms

of the lengths of its four sides and the value of its four

internal angles. If, reading clockwise around the figure,

the side-lengths of the quadrilateral are a, b, c, and d,

and the angles between the edges are A, B, C, and D

(with the angle between edges dand abeing A), then

Bretschneider established that the area Kof the quadri-

lateral is given by:

Here is the semiperimeter of the figure

and θis the average of any two opposite angles in the