a

b

constructible 97

Constructing the sum, difference, product, quotient, and roots of

aand b

regular hexagon with these primitive tools, the con-

struction of a regular heptagon (a seven-sided polygon)

is impossible. C

ARL

F

RIEDRICH

G

AUSS

(1777–1855)

proved that a regular n-gon is constructible if, and only

if, nis a number of the form 2kp1p2…pn, with each pi

a distinct

PRIME

of the form 22s+ 1 (such as 3, 5, 17,

257, and 65,537.) Although one can bisect an angle

with straightedge and compass, the problem of

TRI

-

SECTING AN ANGLE

is unsolvable. The two classical

problems of

SQUARING THE CIRCLE

and

DUPLICATING

THE CUBE

also cannot be solved.

Constructible Numbers

A real number ris said to be constructible if, given a

line segment on a page deemed to be of unit length, it

is possible to construct from it a line segment of

length rusing only the tools of a straightedge and a

compass. For instance, the number 2 is constructible.

(Given a line segment AB of length one, use the

straightedge to extend the length of the line. Draw a

circle of radius equal to the length of AB, centered

about B, to intersect the line at a new point C. Then

the length of AC is 2.) Any positive whole number is

constructible.

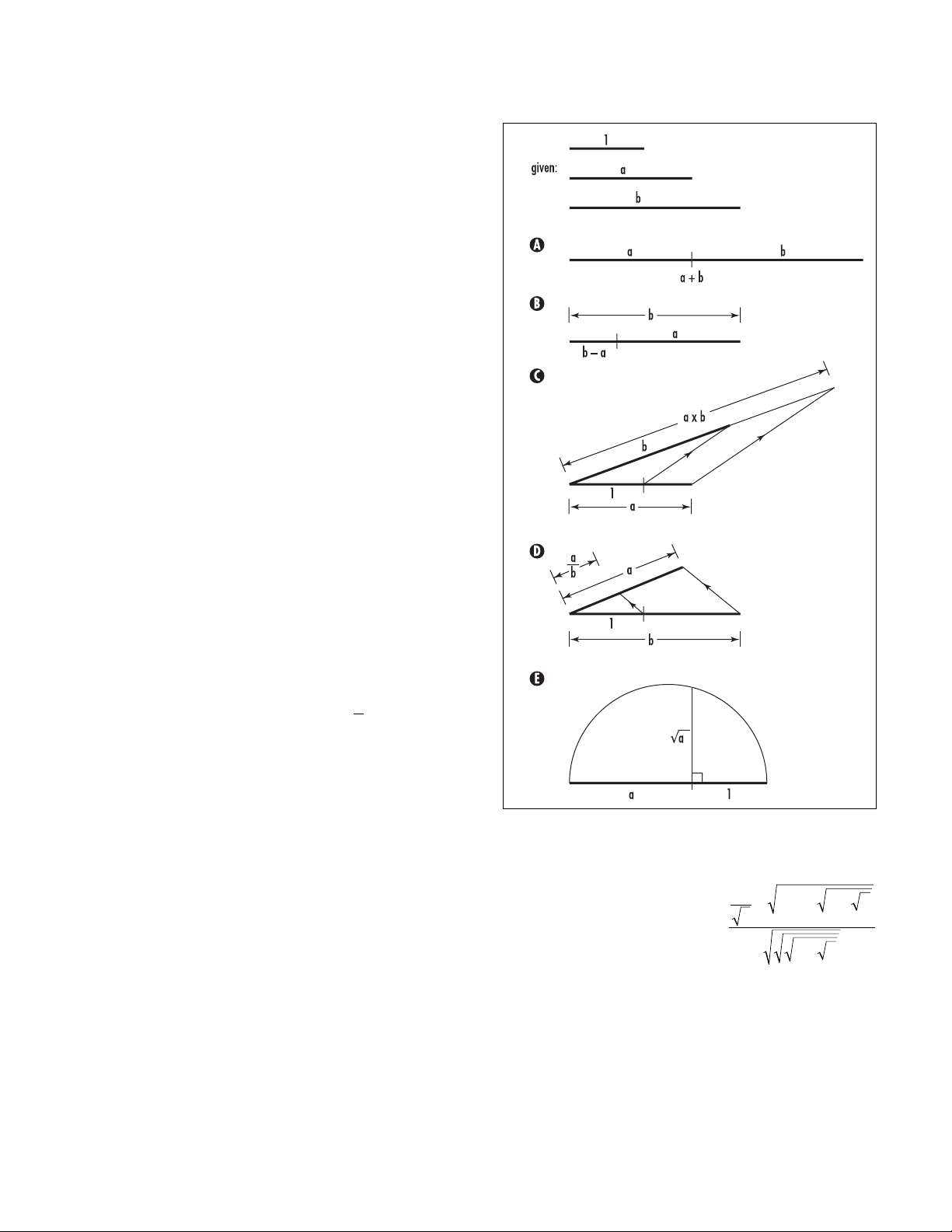
Suppose aand bare two constructible numbers

with b> a. (That is, given a line segment of length 1,

we can also produce line segments of lengths aand b.)

Then the following is true:

The numbers a+ b, b – a, a ×b, , and √

–

aare

constructible.

The diagram at right indicates how to construct these

quantities.

(In the third and fourth diagrams, draw lines par-

allel to the lines connecting the endpoints of the two

segments of lengths aand b. Examination of similar

triangles shows the segments indicated are indeed of

lengths a×band a/b, respectively. For the fifth dia-

gram, add lines to produce a large right triangle

within the circle with the diameter of length a+ 1

as hypotenuse. Application of P

YTHAGORAS

’

S THEO

-

REM

shows that the segment indicated is indeed of

length √

–

a.)

It follows now that any rational number is con-

structible as is any number that can be obtained from the

rationals by the application of a finite number of addi-

tions, subtractions, multiplications, divisions, and square

roots. (For instance, the number

is constructible.) Mathematicians have proved that these

are the only types of real numbers that are constructible.

Mathematicians have also proved that any number that

is constructible is an

ALGEBRAIC NUMBER

. As π, for

instance, is not algebraic, it is not constructible.

See also

AAA

/

AAS

/

ASA

/

SAS

/

SSS

.