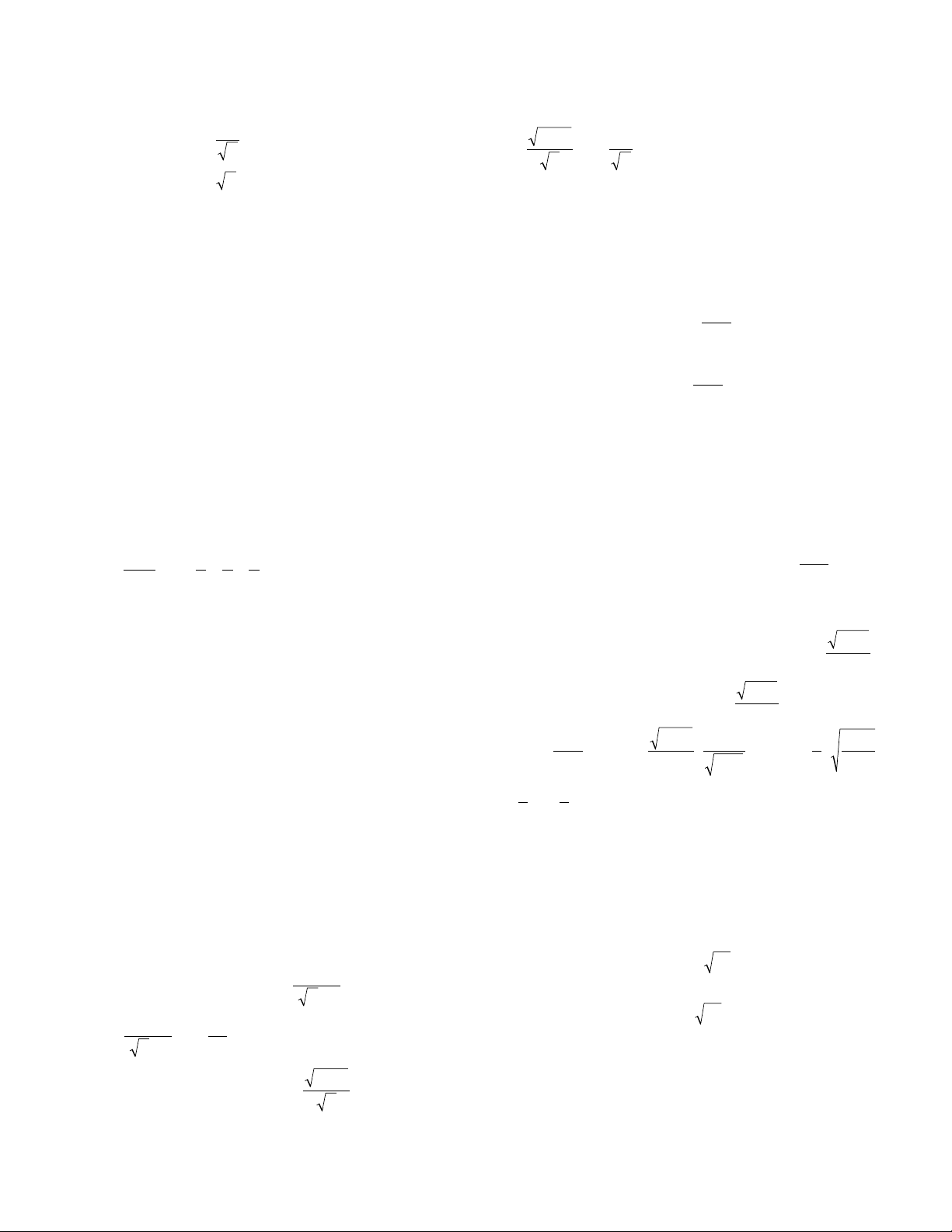
convergent series 103
3
3
3
and so Sn→∞as ngrows.
There are a number of tests to determine whether
or not a given series converges.
The nth-Term Test
If a series converges, then it must be the
case that limn→∞an= 0. Consequently, if the
terms anof the series do not approach zero,
then the series must diverge.
To see why this is true, note that Sn= a1+ a2+…+an–1 +an
= Sn–1 + an. If the partial sums converge to L, then we
must have that limn→∞ an= limn→∞(Sn– Sn–1) = L–L= 0.
This test shows, for example, that the series
diverges because the terms
of the series do not become small.
The Comparison Test
This test applies only to series with positive terms.
A series with positive terms converges if
each term anof the series is less than or equal
to the terms of another series with positive
terms already known to converge.
A series with positive terms diverges if
each term anof the series is greater than or
equal to the terms of another series with posi-
tive terms already known to diverge.
For example, the series converges because
, a series which we already know
converges. The series diverges, since
, which we know diverges.
The Ratio Test
This test applies only to series with positive terms.
A series with all terms positive:
i. converges if exists and equals
a value smaller than 1
ii. diverges if exists and equals
a value greater than 1
If the limit in question actually equals 1, then
nothing can be concluded from this test.
This test was first developed by French mathematician
A
UGUSTIN
-L
OUIS
C
AUCHY
(1789–1857). It is proved in
CALCULUS
texts by making clever comparison to a
GEOMETRIC SERIES
. (Briefly, if for all terms ,
then a2≤ra1, a3≤ra2≤r2a1, a4≤ra3≤r3a1, etc., and
so a1+ a2+ a3+ a4+… ≤a1(1 + r+ r2+ r3+…), which
converges.) Consider, for example, the series .
Here the nth term is given by , and we have:
. By the ratio test, this series converges.
The Root Test
This test applies only to series with positive terms.
A series with all terms positive:
i. converges if exists and equals
a value smaller than 1
ii. diverges if exists and equals
a value greater than 1
If the limit in question actually equals 1, then
nothing can be concluded from this test.
limnn
na
→∞
limnn
na
→∞
an
n=
∞
∑
1
=⋅=<
1
11
1
lim lim lim
nn
nnn
n
n
a
a
n
n
n
n
→∞ +→∞ +→∞
=+⋅+=⋅
+
+
1
1
2
3
3
1
1
3
2
1
an
nn
=+1
n
n
n
+
=
∞
∑1
3
1
a
ar
n
n
+≤<
11
limnn
n
a
a
→∞ +1
limnn
n
a
a
→∞ +1
an
n=
∞
∑
1
n
nn
nn
+>
=
∞
=
∞
∑∑
71
5
11
n
n
n
+
=
∞
∑7
5
1
1
2
1
2
11
()nn
nn
n=
∞
=
∞
∑∑
<
1
2
1()nn
n=
∞
∑
an
n=
∞
∑
1
an
n=
∞
∑
1
n
n
n
−=++++
=
∞
∑101
2
2
3
3
4
1L
an
n=
∞
∑
1
n
n
n
=
=