critical path 109

Task diagrams

and zis a similar ratio of determinants:

In a general situation, Cramer’s rule states:

If Ais the matrix of coefficients of a system of

linear equations, then the value of the ith vari-

able xiin that system of equations is:

provided the determinant of Ais not zero.

Here Aiis the matrix Awith the ith column

replaced with the column of values of the set

of equations.

Notice that Cramer’s rule shows that there can only be

one solution to a system of equations for which the

determinant of the coefficient matrix is nonzero.

In the study of determinants, Cramer’s rule is used

to prove that a matrix Ais invertible if, and only if, its

determinant is not zero.

critical path Suppose that we are given a sequence of

tasks that need to be accomplished in order to complete

a large project, such as building a house or publishing

an encyclopedia, and suppose that these tasks have the

following properties:

1. There is an order of precedence for certain tasks.

2. Some tasks can be carried out simultaneously.

3. The duration of each task is known.

Then the critical path for the project is the longest (in

time) chain of tasks that must be completed in the spec-

ified order. The critical path thus puts a bound on the

minimum amount of time it takes to complete the

entire project.

For example, consider the project of preparing

hamburgers and salad for an evening meal. The follow-

ing table describes the tasks that must be completed,

their prerequisite tasks, and their duration.

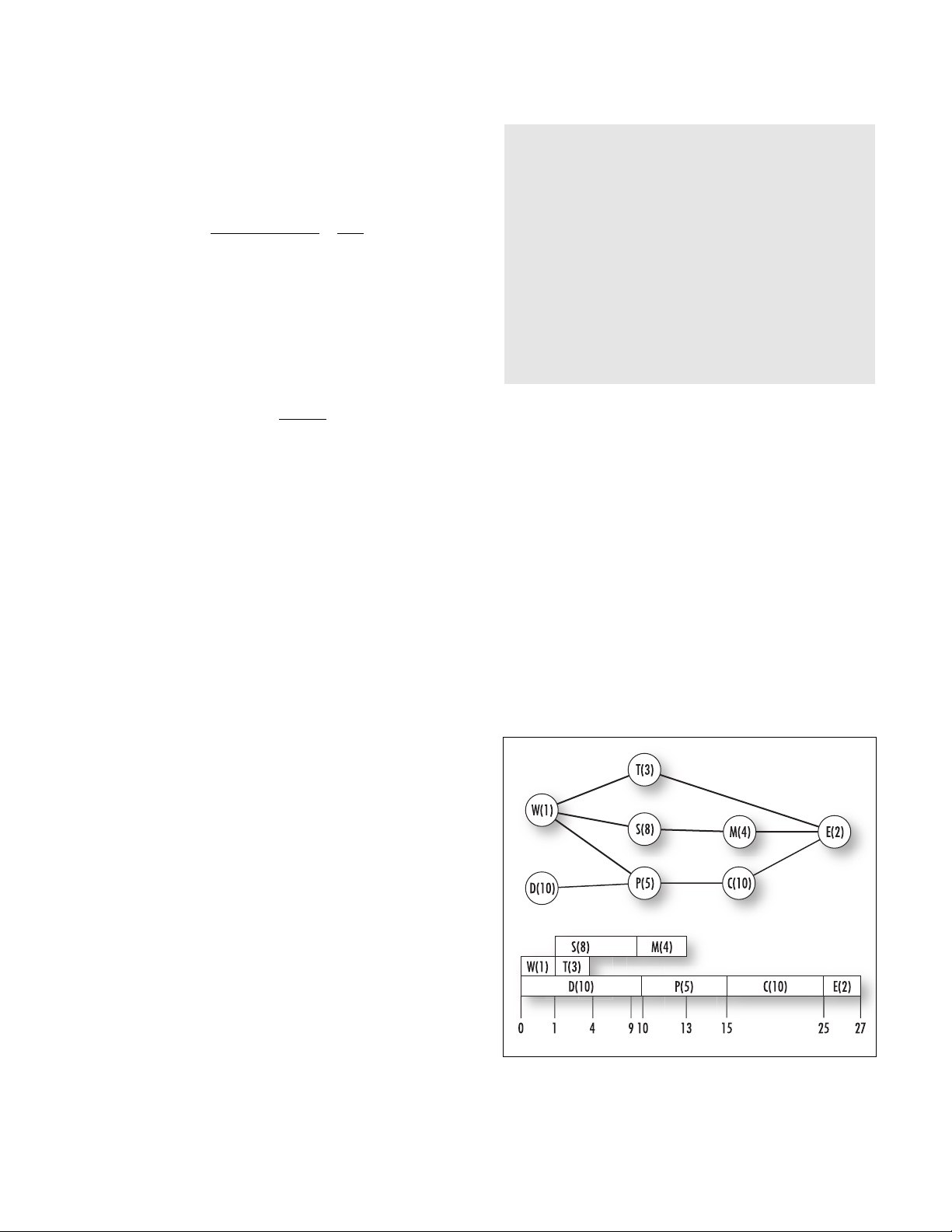
The top diagram below provides a useful

schematic of the ordering of the tasks. (Their times

are written in parentheses.) We see from it that the

longest chain, that is, the critical path of the project,

is the sequence D-P-C-E requiring 27 min to com-

plete. That all the tasks in this example can indeed be

accomplished in exactly 27 min is demonstrated in

the second diagram. In general, there is no guarantee

that the time dictated by the critical path is actually

attainable.

Computers are used to look for critical paths in

complex projects.

See also

OPERATIONS RESEARCH

.

Time to Complete Prerequisite

TASK (in minutes) Tasks

W: wash hands 1 None

D: defrost hamburger 10 None

P: shape meat into patties 5 W, D

C: cook hamburgers 10 P

S: wash and slice 8 W

salad items

M: mix salad 4 S

T: set table 3 W

E: serve meal 2 C, M, T